MOA中RandomTreeGenerator[Basic]
2012-10-26
简介
RandomTreeGenerator是一个数据流(stream)产生器,它首次提出于:
P.Domingos and G. Hulten. Mining high-speed data streams. In KDD, 2000.
它的基本原理:基于一棵随机产生的树,来生成Instance数据。关键点:
- 怎样产生一个随机树?
- 在这棵随机数上,怎样生成
Instance?
下面我们来一一说明。
产生随机树
随机选取属性,作为判断条件,来进行分裂;在最终的leaf上,随机标记一个Class;即可获得一棵随机树,因为在生成过程中,树的中间节点进行属性判断和分裂,因此准确的说,生成的是一棵决策树(decision tree)。如下图所示:
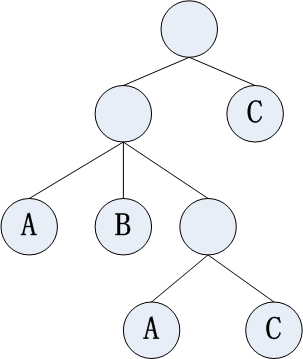
说明:上图表示一棵决策树(decision tree),Instance的Class共计有A B C 3类,均已经标记在leaf上。这棵树上,未标记Class的节点,是中间节点,在其上进行条件判断和分裂。
生成Instance
在讨论如何生成Instance之前,先说明一下,Instance的数学表示形式:< x,y>。其中, x 是一个属性值的向量,y是class的值。例如:Instance: <(1,2,3),A>,表示:属性1=1,属性2=2,属性3=3,并且Class=A的一个Instance。
好了,有了这些说明,那如何利用 “产生随机数” 中获得的随机决策树,来生成Instance呢?
具体分为2步:
- 随机生成一个属性值的向量 x;
- 利用向量 x 中的属性值,去决策树中判断对应的 y 值(class值); 至此,获得了一个Instance < x ,y>
补充
科学实验中,注重实验结果的__可再现__、__可重现__性;为了保证 Instance 的可再现,需要保证__随机决策树__的可再现。在MOA中,这些都已经实现,使用的是JAVA中Random类。
在实际的程序中,随机决策树的产生,可以进行设定一些参数,来进行约束:
| 参数 | 说明 |
|---|---|
| -r | 保证 随机决策树 的再现性,只要此值相同,产生的随机树,即相同 |
| -i | 保证 Instance 的再现性,如果 -r 值相同,并且 -i 值相同,则产生的instance相同 |
| -c | 产生的class个数 |
| -o | 属性中,离散型属性的个数 |
| -u | 属性中,数值型(连续型)属性的个数 |
| -d | 树的深度 |
| -l | 首次存在 leaf 节点的level |
| -f | 每层中leaf 节点所占的比重 |
参考来源
- MOA:StreamMining.pdf PART: 2.5.1 Random Tree Generator
- MOA:Manul.pdf PART: 6.2.7 generators.RandomTreeGenerator
原文地址:https://ningg.top/moa-random-tree-generator/