算法系列:历史算法汇总
2017-04-30
0.概要
所有算法问题的分析汇总。
1.数组
1.1.连续子数组的和为指定值,连续子数组的最大长度
题目:
连续子数组,和为固定值 key,求连续子数组的最大长度(LeetCode 525)
分析:
- 示例:数组{1,3,4,5,8,5},目标值 key 为 13,则,连续子数组的最大长度为 4,对应的连续子数组为{1,3,4,5}
- 思路A:基本思路
- 思路:找出所有子数组,判断哪些的 sum 为 key,求出其中,最大的长度
- 时间复杂度:
O(n^2)
- 思路B:
- 思路:连续子数组的和,我们就计算「前缀和」,然后遍历前缀和 prefixSum,逐个判断对应的 currentValue = prefixSum - key 是否存在「前缀和」中,并更新最大的 len
- 时间复杂度:
O(n) - 空间复杂度:
O(n)
举例,arr = {1,3,4,5,8,5},和 key 为13,最长子数组为{1,3,4,5}
| arr | 1 | 3 | 4 | 5 | 8 | 5 |
|---|---|---|---|---|---|---|
| sum | 1 | 4 | 8 | 13 | 21 | 26 |
| index | 0 | 1 | 2 | 3 | 4 | 5 |
特别注意,需要设定一个基准点(sum,index) = {0,-1},以此覆盖涵盖第一个元素的情况
具体代码:
/**
* 题目: 连续子数组,和为固定值 key,求连续子数组的最大长度
*
* TODO: 整理独立的博文
*
* 备注:
* 下述代码, 「Map中」只保留了「第一次出现取值的 prefixSum」, 这并不会影响最终的 maxLen,
* 因为 maxLen 计算过程中, 利用了「后续出现取值的 prefixSum」。
*/
public class SubArraySumKey {
public static int subArraySumKeyMaxLen(int[] array, int destKey) {
// 1. 边界判断
if (null == array) {
return -1;
}
// 2. 求数组的「前缀和」,并保存到 Map 中, 同时, 统计最大的 Len
HashMap<Integer, Integer> prefixSumArray = new HashMap<>();
int prefixSum = 0;
// a. 设置基准点
prefixSumArray.put(0, -1);
int maxLen = 0;
for (int index = 0; index < array.length; index++) {
prefixSum += array[index];
// b. 判断目标取值是否存在, 若存在, 则,更新 maxLen
int delta = prefixSum - destKey;
if (prefixSumArray.containsKey(delta)) {
int deltaIndex = prefixSumArray.get(delta);
maxLen = Math.max(index - deltaIndex, maxLen);
}
// c. 判断当前「前缀和」, 是否存在, 若不存在, 则, 添加到 HashMap 中
if (!prefixSumArray.containsKey(prefixSum)) {
prefixSumArray.put(prefixSum, index);
}
}
return maxLen;
}
public static void main(String[] args) {
int[] inputArray = {1, 3, 4, 5, 8, 5};
int destValue = 13;
int result = subArraySumKeyMaxLen(inputArray, destValue);
System.out.println(result);
}
}
扩展:给定一个字符串只包含0和1,找出一个最长的连续子串,使得0和1的个数相等。
这里只需要将0变为-1,问题就转化为和为0的最长子数组问题
参考资料:
- https://blog.csdn.net/qq_26305015/article/details/78251534
- https://www.cnblogs.com/liujinhong/p/6472580.html
1.2.零钱兑换问题:给定面额和目标金额,求可等额兑换的最小的硬币数量
题目:
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
Note:假设硬币面额种类 k 种,最后的目标总金额为 n。
思路:
- 暴力方法:
- 基本思路:找出每种面额的硬币,最大的数量,在这些数量中,进行暴力组合。
- 时间复杂度:
(n/k )^k,差不多算O(2^k)
- 降低问题规模:
- 基本思路:动态规划, f(n) = min{f(n-i)} +1),其中 i 取值为硬币面额。
- 本质就是求:amount 目标金额是否属于上述「序列」。
具体,上述序列,采用字典树,自顶向下分析:
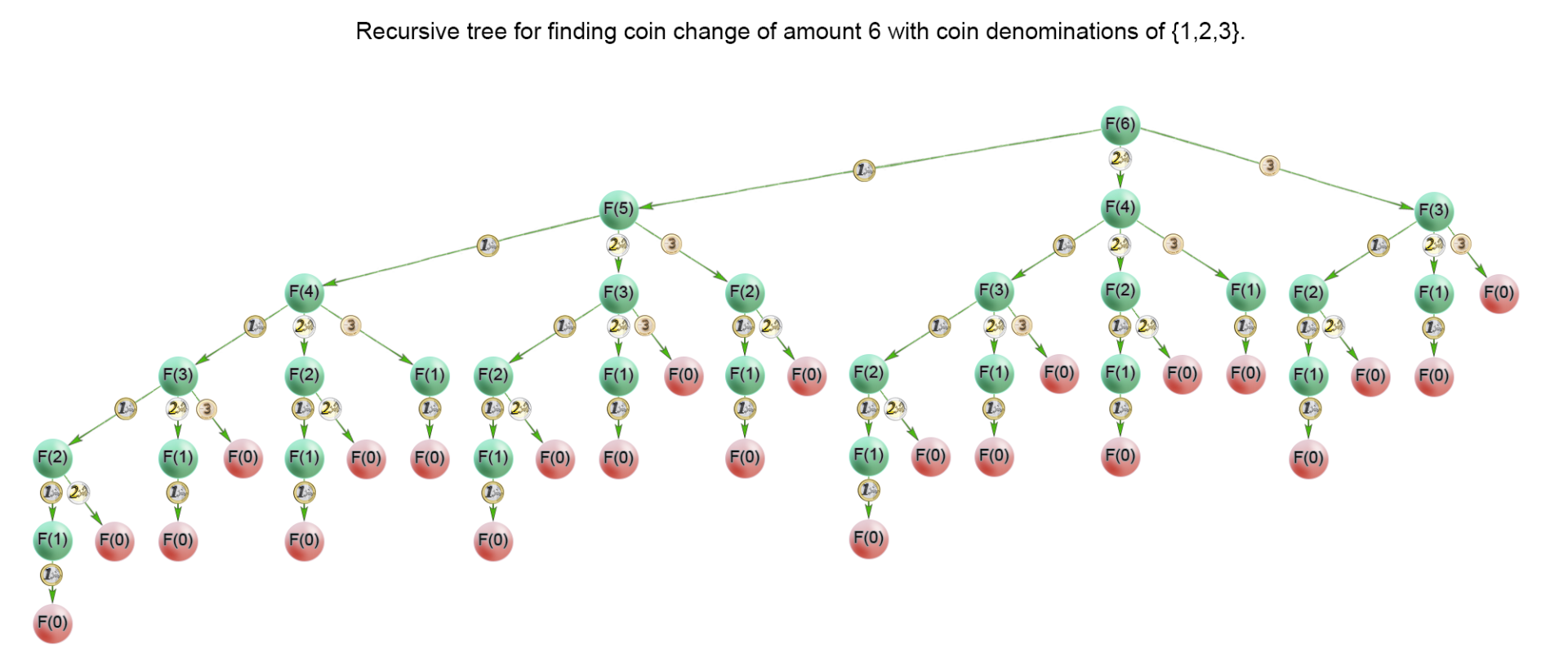
示例代码:
/**
* 自顶向下,迭代计算。
*
* @param coins 不同面额的数组
* @param amount 兑换金额
* @return 所需硬币的最少数量
*/
public static int coinChangeLoop(int[] coins, int amount) {
// 边界判断
if (null == coins || amount <= 0) {
return -1;
}
// 终止条件
int len = coins.length;
for (int coin : coins) {
if (coin == amount) {
return 1;
}
}
// 迭代
int[] deltaAmounts = new int[len];
for (int i = 0; i < len; i++) {
deltaAmounts[i] = coinChangeLoop(coins, amount - coins[i]);
}
// 返回结果
int min = Integer.MAX_VALUE;
for (int i = 0; i < len; i++) {
int currValue = deltaAmounts[i];
// 此处有:合规匹配
if (currValue > 0) {
if (currValue < min) {
min = currValue;
}
}
}
return (min == Integer.MAX_VALUE) ? -1 : (min + 1);
}
所以,采用自底向上解决:

示例代码:
/**
* 自底向上,逐个计算潜在金额,并匹配目标金额.
*
* 实现:使用「外部存储」,下标表示目标金额,存储值表示最少硬币数量.
*
* @param coins 不同面额的数组
* @param amount 兑换金额
* @return 所需硬币的最少数量
*/
public static int coinChange(int[] coins, int amount) {
// 边界判断
if (null == coins || amount <= 0) {
return -1;
}
// 借助外部存储: 存储金额对应的硬币数量
int max = amount + 1;
int[] dps = new int[amount + 1];
Arrays.fill(dps, max);
// 设置起始条件
dps[0] = 0;
// 从前向后,逐步更新
for (int i = 1; i <= amount; i++) {
for (int coin : coins) {
int delta = i - coin;
if (delta < 0) {
continue;
}
dps[i] = Math.min(dps[i], dps[delta] + 1);
}
}
return (dps[amount] > amount) ? -1 : dps[amount];
}
参考资料:
1.3.拦截导弹,输出可以拦截捣蛋的数量
题目:
问题描述:
- 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。 输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式 :
- 一行,为导弹依次飞来的高度
输出格式
两行,分别是最多能拦截的导弹数与要拦截所有导弹最少要配备的系统数
- 分析:本质是,求「最长递增子序列」的长度,因为「当前元素之前」出现「小于当前元素」的「元素」,则,需要增加一个导弹拦截系统
样例输入
- 389 207 155 300 299 170 158 65
样例输出
6
2
分析:
本质:求数组的「最长递简子序列」的长度,以及「最长递增子序列」的长度
2 种解决办法:
- 方法 A:基础方法,暴力获取「所有的子序列」,然后判断哪个是「最长的递增子序列」,时间复杂度
O(2^n) - 方法 B:动态规划,降低问题规模,判断一下是否存在「后效性」,具体细节
- 定义:
max[i]:第 i 位之前,最长递减子序列的长度maxSuffix[i]:第 i 位之前,且包含第 i 位的,最长递减子序列的长度
- 状态转移函数:第 i +1 位,初始 max[i+1]设置为 1
- max[i + 1] = Max{max[i+1], maxSuffix[i + 1] },分为 2 个维度(包含 i + 1 位,不包含 i + 1 位)
- maxSuffix[i + 1] = Max{ max[k] } + 1,其中 k 属于[0, i],且 max[k] >= array[i + 1]
- 定义:
具体的代码:
public static int subArrayDescMaxLen(int[] array) {
// 边界判断
if (null == array) {
return 0;
}
// 定义:max[i]
int len = array.length;
int[] max = new int[len];
Arrays.fill(max, 1);
for (int i = 0; i < len; i++) {
// 状态转移函数:回溯
for (int j = 0; j < i; j++) {
if (array[i] <= array[j]) {
max[i] = Math.max(max[i], max[j] + 1);
}
}
}
return max[len - 1];
}
参考资料:
- https://leetcode.com/problems/longest-increasing-subsequence/
- https://blog.csdn.net/EbowTang/article/details/50527709
- https://blog.csdn.net/mrwangweijin/article/details/78319407
1.4.股票最大收益
参考资料:
1.5.数组中,两数和为指定值,求这两个
参考资料:
1.6.水池,最大蓄水量
本质分析:
- 特性:单调性,从 2 端开始,各放置一个指针
- 如果 height(left) < height(right)
- 则,如果保持 left 位置不变,无论如何 减小 right 位置,得到的「水池容量」都会比当前取值更小,具备单调性
- 因此,此种情况下,只能「增加」left 位置,尝试获取更大的「水池容量」
- 动态规划:
- 初始状态:数组两端,放置 2 个指针,left = 0,right = len-1
- 迭代条件:height(left) < height(right) 时,增加 left 位置,否则,减小 right 位置
- 终止条件:left >= right
参考资料:
- http://www.voidcn.com/article/p-rqzxxfuf-bkg.html
- https://blog.csdn.net/wzy_1988/article/details/17248209
1.7.加油站问题,寻找起点
题目:
沿环形路线有N个加油站,其中气体在车站i是量是gas[i]。你有车有无限容量的气罐,从加油站i到下一个加油站站点i+1,要消耗cost[i]的气体。你开始旅程时,气罐是空的。回到起始加油站的指数,选择一个起点开始旅游,如果你能在周围环形旅行一次,就返回开始的加油站索引,否则返回-1。
分析:
- 寻找后段「汽油富余」的入口
核心思想:
- 总加油量要大于总消耗量。
- 如果在第 i 站无法到达第 i + 1 站,那么从 i-1,i-2……等第 i 站前面的站开始出发必然都到不了第 i+1 站。所以只有可能从第i+1站开始,才有可能走一圈。
- 如果低 i+1站能够到达第n站,并且总加油量大于总消耗量,那么从 i+1站到第n站结余的油量必然能够满足从0站到 i+1站的需求。(0和n是同一个站)。
示例代码:
TODO
参考资料:
- https://blog.csdn.net/sk199048/article/details/39049249
- https://blog.csdn.net/JackZhang_123/article/details/78008439
2.链表
2.1.指定区间内,翻转链表
题目:
链表翻转,给定指定的区间,翻转链表(LeetCode 92)
分析:
跟单独的链表翻转不同,可以采用「插入法」,遍历一个节点,就在链表中,插入一几个节点,实现翻转。
具体思路:
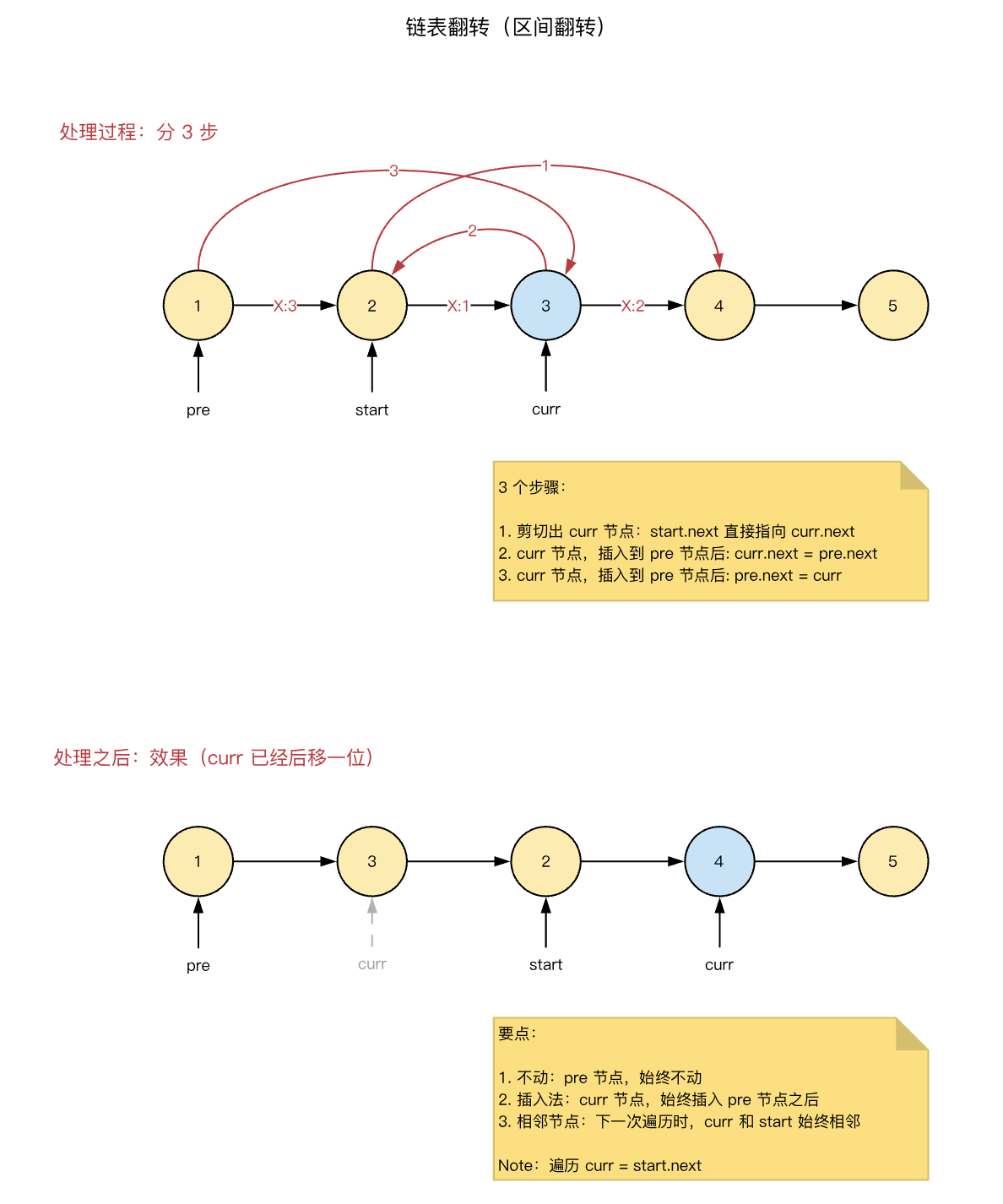
具体步骤:
- 获取开头位置指针 pre、start、curr
- 插入法:逐个遍历,然后在 pre 后,插入节点 curr
- 不变的节点:pre 指向的节点
- 邻近节点:start 和 curr 指向的节点
具体示例代码:
/**
* 题目:翻转链表的指定区间。
*/
public class ReverseSegmentList {
/**
* 根据给定的位置,进行链表的局部翻转
*
* @param head 链表头
* @param m 第 m 个节点
* @param n 第 n 个节点
* @return 翻转之后的节点
*/
public static Node reverseList(Node head, int m, int n) {
// 边界判断
if (null == head) {
return null;
}
if (m >= n) {
return head;
}
// a. 获取 pre 节点
Node bufNode = new Node(0);
bufNode.next = head;
Node pre = bufNode;
// 特别说明:pre 停留在 m 编号之前
for (int index = 1; index < m; index++) {
pre = pre.next;
}
// b. 插入法,逐次遍历节点,并插入
Node start = pre.next;
Node curr = start.next;
// 特别说明:插入 n-m 次
for (int index = m; index < n; index++) {
start.next = curr.next;
curr.next = pre.next;
pre.next = curr;
curr = start.next;
}
return bufNode.next;
}
public static void main(String[] args) {
Node oriList = ListUtils.constructNodeList(8);
ListUtils.printList(oriList);
int m = 2;
int n = 5;
Node result = reverseList(oriList, m, n);
ListUtils.printList(result);
}
}
参考资料:
- https://blog.csdn.net/m0_37885286/article/details/81877745
- https://blog.csdn.net/u010347226/article/details/63266631
2.2.链表,整数求和
参考资料:
- https://blog.csdn.net/PengXR2017/article/details/56490567
- https://leetcode.com/problems/add-two-numbers/discuss/1059/My-accepted-Java-solution
2.3.链表,排序
题目:
单链表,归并排序
考察点:整体思路,归并排序算法的掌握,归并排序算法的迁移能力,手写代码边界判断是否清晰。
题目详细描述:
/**
* 题目:单链表,排序(升序)
*
*/
// 已经提供下面数据结构,表示单个链表节点
class Node {
public int value;
public Node next;
public Node(int value) {
this.value = value;
this.next = null;
}
}
// 实现下面方法,对单链表,进行升序排列
Node sortList(Node head);
示例(java):
/**
* 题目:单链表,排序(升序)
*
* 分析:
* 1. 方案A:选择排序,时间复杂度 O(n^2)
* 2. 方案B:归并排序,时间复杂度 O(nlg(n))
*
* Created by guoning on 17/8/23.
*/
public class SortList {
public static void main(String[] args) {
// 1. 构造列表
Node node = constructNodeList(4);
// 2. 排序
Node result = sortList(node);
// 3. 输出
for (Node currNode = result; currNode != null; currNode = currNode.next) {
System.out.println(currNode.value);
}
}
private static Node constructNodeList(int num) {
Node node = null;
Node currNode = null;
Random random = new Random();
for (int index = 0; index < num; index++) {
int value = random.nextInt(100);
Node newNode = new Node(value);
if (node == null) {
node = newNode;
currNode = node;
} else {
currNode.next = newNode;
currNode = currNode.next;
}
}
return node;
}
static class Node {
public int value;
public Node next;
public Node(int value) {
this.value = value;
this.next = null;
}
}
// 归并排序
// 1. 中间节点:找到中间节点,将链表拆为 2 部分
// 2. 递归:对 2 部分分别进行排序
// 3. 合并:合并 2 部分有序链表
private static Node sortList(Node head) {
// 边界判断
if (null == head || null == head.next) {
return head;
}
// 1. 中间节点
Node mid = getMiddleNode(head);
// 破坏链表结构
Node second = null;
if (mid == null) {
second = null;
} else {
second = mid.next;
mid.next = null;
}
// 2. 递归:分别对 2 个链表排序
Node firstHead = sortList(head);
Node secondHead = sortList(second);
// 3. 合并:2 个有序列表,合并
return mergeSortedList(firstHead, secondHead);
}
// 获取中间节点
private static Node getMiddleNode(Node head) {
// 边界判断
if (null == head || null == head.next) {
return head;
}
// 2 只有 2 个节点
if (head.next.next == null){
return head;
}
// 2 个指针:一个每次 2 步,一个每次 1 步
Node first = head;
Node second = head;
while (second != null && second.next != null) {
first = first.next;
second = second.next.next;
}
return first;
}
// 合并 2 个有序列表
private static Node mergeSortedList(Node firstHead, Node secondHead) {
// 边界条件
if (null == firstHead) {
return secondHead;
}
if (null == secondHead) {
return firstHead;
}
// 2 个指针:遍历 2 个链表,调整链表指向关系
if (firstHead.value < secondHead.value) {
firstHead.next = mergeSortedList(firstHead.next, secondHead);
return firstHead;
} else {
secondHead.next = mergeSortedList(firstHead, secondHead.next);
return secondHead;
}
}
}
3.树
3.1.二叉查找树,只有2个节点被交换过,找出来并修正
题目:
重构二叉查找树,找出被交换的 2 个节点(LeetCode 99)
分析:(基本思路)
- 二叉查找树,中序遍历后,得到一个升序的数组
- 两个节点被交换,则,会出现 2 个逆序数
- 找到这两个逆序数,然后,交换即可
详细分析:
- 如果将一个有序数组中的两个元素进行交换了,如何找出这两个数?(找到后还原是简单的)
- 如对于数组1,2,7,4,5,6,3,8,9,如何判断是哪两个元素发生了交换呢?
- 不难发现,新的数组中存在两对逆序并相邻的数字,即7,4和6,3,造成这出现的原因,正是发生了一次交换,由于一定是较小的数换到了较大数的位置(向后),较大的数换到了较小数的位置(向前)。所以在这两对中,我们可以简单的判断出:是前一对的较大数和后一对的较小数发生了交换。
要求:
- 空间复杂度为
O(1) - Note:使用递归遍历,本质也是使用了「栈」,空间复杂度为
O(lg(N))
本质:
- 找出 2 个不满足升序条件的「节点」,最后交换即可。
示例代码:
/**
* 题目:重构二叉查找树,找出被交换的 2 个节点
*/
public class RecoverTree {
private static TreeNode firstNode = null;
private static TreeNode secondNode = null;
private static TreeNode preNode = null;
/**
* 修复二叉查找树。
*
* @param root 二叉查找树的根节点。
*/
public static void recoverTree(TreeNode root) {
if (null == root) {
return;
}
// 中序遍历:找出 2 个逆序的节点
inOrderTraverse(root);
int tmp = firstNode.value;
firstNode.value = secondNode.value;
secondNode.value = tmp;
}
/**
* 中序遍历二叉查找树,同时,判断逆序节点
*
* @param root 二叉查找树的根节点
*/
public static void inOrderTraverse(TreeNode root) {
if (null == root) {
return;
}
inOrderTraverse(root.left);
if (preNode != null) {
if (preNode.value > root.value) {
if (firstNode == null) {
firstNode = preNode;
secondNode = root;
} else {
secondNode = root;
}
}
}
preNode = root;
inOrderTraverse(root.right);
}
}
参考资料:
- https://www.jiuzhang.com/solution/recover-binary-search-tree/
- http://www.cnblogs.com/yuzhangcmu/p/4208319.html
- http://fisherlei.blogspot.com/2012/12/leetcode-recover-binary-search-tree.html
- https://www.tianmaying.com/tutorial/LC99
3.2.二叉树中,路径和为固定值
题目:
二叉树,路径和为固定值的所有路径
分析:
- 树,适合使用递归,逐层递归,每次缩小问题,同时,设定好终止条件
具体代码:
/**
* 题目:二叉树,路径和为固定值
*
* 1. 判断:是否存在路径
* 2. 输出满足条件的路径
*/
public class PathSum {
/**
* 判断:是否存在路径,路径和为指定值.
*/
public static boolean hasPathSatisfySum(TreeNode root, int sum) {
if (null == root) {
return false;
}
// 终止条件:叶子节点
if (root.left == null && root.right == null) {
if (sum == root.value) {
return true;
}
}
// 迭代判断
int delta = sum - root.value;
boolean leftResult = hasPathSatisfySum(root.left, delta);
boolean rightResult = hasPathSatisfySum(root.right, delta);
return leftResult || rightResult;
}
private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
private ArrayList<Integer> list = new ArrayList<Integer>();
/**
* 输出满足条件的路径
* @param root
* @param target
* @return
*/
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
if(root == null){
return listAll;
}
list.add(root.value);
// 终止条件
int delta = target - root.value;
if(target == 0 && root.left == null && root.right == null){
listAll.add(new ArrayList<Integer>(list));
}
// 迭代
FindPath(root.left, delta);
FindPath(root.right, delta);
// 移除当前节点
list.remove(list.size()-1);
return listAll;
}
}
参考资料:
- https://blog.csdn.net/qq_25827845/article/details/73565502
- https://blog.csdn.net/weixin_38368941/article/details/80296641
3.3.二叉树,遍历(非递归)
几种场景:
- 前序遍历:非递归
- 中序遍历:非递归
- 后续遍历:非递归
3.3.1.二叉树,前序
基本思路:
借助「栈」进行实现,核心思路:
初始化:root 入栈
循环:
出栈 1 个节点、记录
右、左,子节点入栈
- 终止条件:
- 「栈」为空
具体示意图:
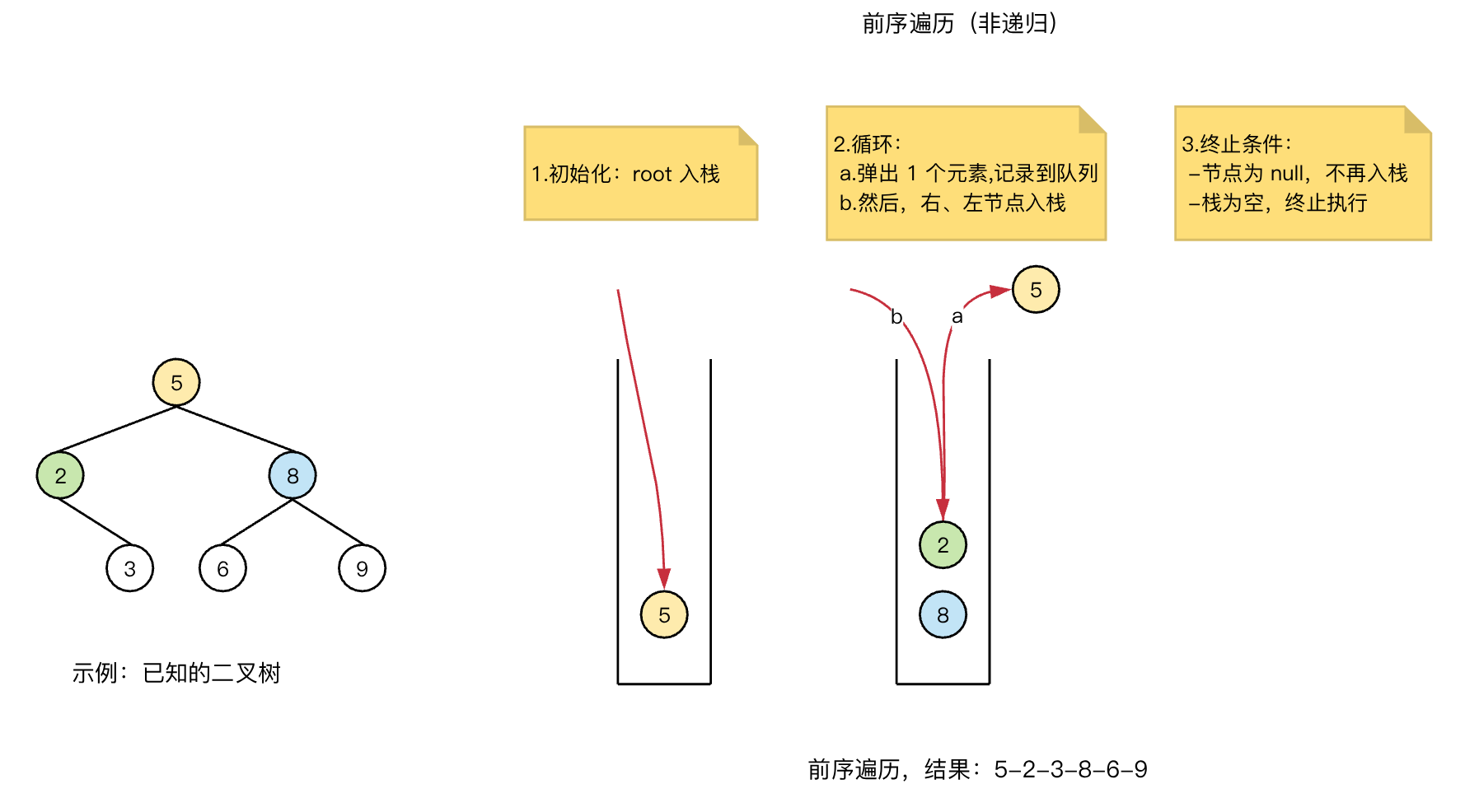
示例代码:
/**
* 遍历:前序(非递归,循环方式)
*
* Note:有独立的示意图
*
* @param root 二叉树根节点
* @param result 中序遍历的结果
*/
public static void preOrderTraverseLoop(TreeNode root, List<TreeNode> result) {
Stack<TreeNode> stack = new Stack<>();
// 基本逻辑:
// 1. 初始化:root 入栈
// 2. 循环逻辑:弹出一个节点,并将右、左子节点入栈
// 3. 终止条件:节点为 null,不再入栈,stack 为空,终止处理
if (null == root) {
return;
}
stack.push(root);
while (!stack.isEmpty()) {
// a. 弹出元素
TreeNode currNode = stack.pop();
// b. 子节点入栈:右、左节点,入栈
if (null != currNode.right) {
stack.push(currNode.right);
}
if (null != currNode.left) {
stack.push(currNode.left);
}
// c. 节点增加到返回队列
result.add(currNode);
}
}
3.3.2.二叉树,中序
基本思路:
借助「栈」来实现
初始:记录当前节点,为 root 节点
循环:
「当前节点」非 null,则入栈,并,将「左子节点」设置为「当前节点」
如果「当前节点」为 null,则,弹出一个节点,记录到结果中
以「弹出的节点」的「右子节点」为基准,设置为「当前节点」
- 终止条件:
- 「栈」为空,且,「当前节点」也为空
具体示意图:
TODO
示例代码:
/**
* 遍历:中序(非递归,循环方式)
*
* @param root 二叉树根节点
* @param result 中序遍历的结果
*/
public static void inOrderTraverseLoop(TreeNode root, List<TreeNode> result) {
Stack<TreeNode> stack = new Stack<>();
// 基本逻辑:
// 1. 初始化:记录当前节点,为 root 节点
// 2. 循环逻辑:
// a. 「当前节点」非 null,则入栈,并,将「左子节点」设置为「当前节点」
// b. 如果「当前节点」为 null,则,弹出一个节点,记录到结果中
// c. 以「弹出的节点」的「右子节点」为基准,设置为「当前节点」
// 3. 终止条件:「栈」为空,且,「当前节点」也为空
if (null == root) {
return;
}
TreeNode currNode = root;
while (!stack.isEmpty() || null != currNode) {
if (null != currNode) {
stack.push(currNode);
currNode = currNode.left;
} else {
TreeNode validNode = stack.pop();
result.add(validNode);
currNode = validNode.right;
}
}
}
参考资料:
- https://blog.csdn.net/u012162613/article/details/41114105
- https://www.cnblogs.com/en-heng/p/6349374.html
3.3.3.二叉树,后序
分析:
- 后序遍历,相对前序、中序,稍微复杂一些,关键点在于:什么时候,允许访问当前节点,下面几种情况
- 情况A:左子节点、右子节点,都不存在
- 情况B:左子节点,刚被访问,右子节点为空,则,可以访问当前节点
- 情况C:右子节点不为空,右子节点,刚被访问,则,可以访问当前节点
- 其他情况:依次将右子节点、左子节点,压入栈中
基本思路:
借助「栈」实现:非空「左子树」循环入栈;「栈顶元素」不出栈,「右子树」非空且未被记录,则以「右子树」更新当前节点,并开始「左子树」循环入栈逻辑;若「栈顶元素」的子节点全部出栈,则,「栈顶元素」出栈
初始化:root 节点,标记为「当前节点」
循环逻辑:
「当前节点」非 null,则,「当前节点」入栈,并且以「左子树」更新「当前节点」
「当前节点」为 null,则,读取「栈顶元素」(不出栈),判断其「右子节点」是否为 null
若「右子节点」为 null,则,「栈顶元素」出栈,并记录为「最近一次记录的元素」
若「右子节点」非 null,则,判断「右子节点」是否为「最近一次记录的元素」
若「右子节点」不为「最近一次记录的元素」,则,以「右子节点」来更新「当前节点」,并继续循环执行
若「右子节点」为「最近一次记录的元素」,则,弹出「栈顶元素」,并输出,同时,更新「最近一次记录的元素」
示例:

具体流程图:
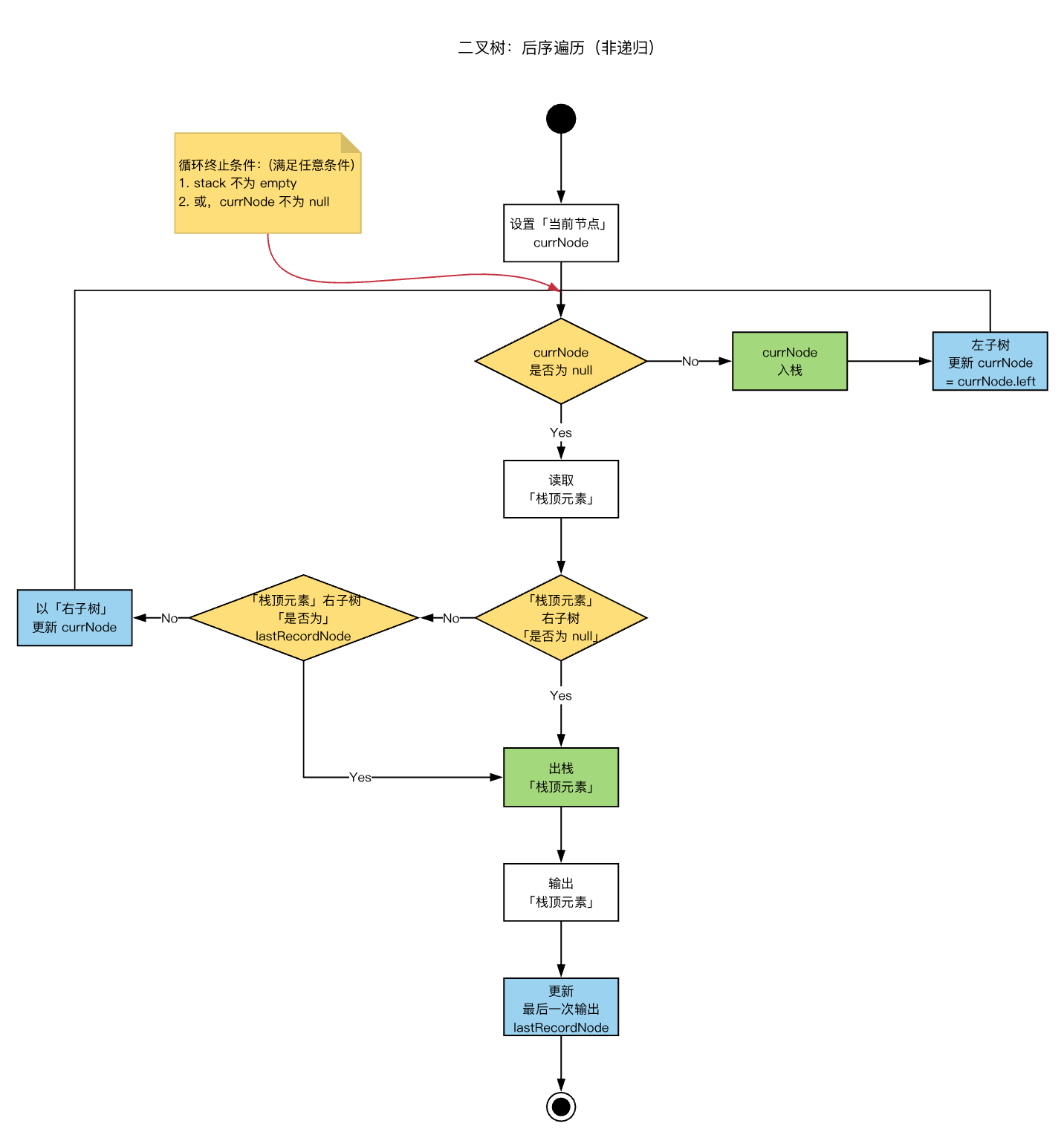
示例代码:
/**
* 遍历:后续(非递归,循环方式)
*
* @param root 二叉树根节点
* @param result 遍历输出的结果
*/
public static void postOrderTraverseLoop(TreeNode root, List<TreeNode> result) {
Stack<TreeNode> stack = new Stack<>();
// 基本逻辑:非空「左子树」循环入栈,顶点不出栈,右子树有效则继续「左子树循环入栈」,若子节点全部出栈则顶部节点出栈
// 1. 初始化:记录当前节点,为 root 节点
// 2. 循环逻辑:
// a. 「当前节点」非 null,则,入栈,并将「左子节点」设置为「当前节点」
// b. 如果「当前节点」为 null,则,查询顶部节点(不弹出),判断其「右子节点」是否为 null or 为「上次输出」的节点,若满足,则,弹出「顶部节点」并输出
// c. 如果「当前节点」为 null,且顶部节点(不弹出),其「右子节点」不为 null,且「未被输出」,则,将其作为「当前节点」,进入循环逻辑
// 3. 终止条件:「栈」为空,且,「当前节点」也为空
if (null == root) {
return;
}
TreeNode currNode = root;
TreeNode lastRecordNode = null;
while (!stack.isEmpty() || currNode != null) {
// a. 「当前节点」不为 null,则,入栈,并以「左子节点」作为当前节点,继续迭代
if (null != currNode) {
stack.push(currNode);
currNode = currNode.left;
} else {
// b. 当前节点为 null,则,查询顶部节点
TreeNode topNode = stack.peek();
if (null != topNode.right && lastRecordNode != topNode.right) {
// 1. 「顶部节点」可以「右子节点」进行递归,则继续递归
currNode = topNode.right;
} else {
// 2. 「顶部节点」满足「出栈条件」,则出栈访问
topNode = stack.pop();
lastRecordNode = topNode;
result.add(topNode);
}
}
}
}
参考资料:
3.3.4.二叉树,二叉搜索树,转换为双向链表
题目:
将「二叉搜索树」,转换为「双向链表」,其中,Node 的 left 为 pre,right 为 next
分析:
- 在「循环方式」的「中序遍历」上,记录「上一次输出的节点」即可。
具体示例代码:
public static TreeNode treeToList(TreeNode root) {
if (null == root) {
return root;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode currNode = root;
TreeNode preNode = null, headNode = null;
while (!stack.isEmpty() || null != currNode) {
if (null != currNode) {
// 左子节点,循环入栈
stack.push(currNode);
currNode = currNode.left;
} else {
// 弹出栈顶元素
TreeNode topNode = stack.pop();
// 标记:head
if (null == headNode) {
headNode = topNode;
}
if (null != preNode) {
preNode.right = topNode;
}
// 更新「前驱节点」
topNode.left = preNode;
preNode = topNode;
// 迭代:右子节点,继续迭代
currNode = topNode.right;
}
}
return headNode;
}
参考资料:
3.4.二叉树,每一层,最右边的元素
题目:
输出二叉树,每一层的最右节点
分析:2 种方法
- 方法 A:借助队列,层次遍历,然后,输出每层最后一个元素
- 方法 B:深度优先 DFS,右侧优先
- 每一层,只有一个节点
- 每一层,从「右」向「左」看到的「第一个节点」,就是目标节点
示例代码:(方法 B,深度优先 DFS)
public static List<TreeNode> rightMost(TreeNode root) {
List<TreeNode> list = new LinkedList<>();
if (null == root) {
return null;
}
rightMost(root, 0, list);
return list;
}
public static void rightMost(TreeNode currNode, int depth, List<TreeNode> list) {
if (list.size() == depth) {
list.add(currNode);
}
// 右侧优先
if (currNode.right != null) {
rightMost(currNode.right, depth + 1, list);
}
if (currNode.left != null) {
rightMost(currNode.left, depth + 1, list);
}
}
参考资料:
- https://goleetcode.io/2018/12/07/tree/199-binary-tree-right-side-view/
- https://blog.csdn.net/jmspan/article/details/51311464
4.数字
4.1.求一个数的开根号取值 Sqrt(x)
题目:
Implement int sqrt(int x).
Compute and return the square root of x.
参考资料:
5.智力
5.1.随机数发生器
题目:
有一个 Random5 随机等概率生成 [1,5] 之间的数字,求构造一个 Random7 随机等概率生成 [1,7] 之间的数字
分析:
- 构造基点:(Random5-1)* 5
- 每个基点,增加增量:Random5
- 总取值:result = (Random5-1)* 5 + Random5,等概率涵盖了[1, 25]
- 结果截取,从上述结果中,只截取 result [1,7] 部分,即可
参考资料:
- https://www.zhihu.com/question/47038069
- https://blog.csdn.net/a83610312/article/details/11864265
- https://blog.csdn.net/furturerock/article/details/6850634
- https://www.growingwiththeweb.com/2014/03/given-random5-implement-random7.html
其他
焦点:一些尚未整理的内容。
Point:直方图中,最大矩形面积
- https://blog.csdn.net/Revivedsun/article/details/52420679
- https://www.jiuzhang.com/solution/largest-rectangle-in-histogram/
Point:滑动窗口,最大值
- https://blog.csdn.net/u012243115/article/details/47035643
- https://blog.csdn.net/ylyg050518/article/details/77834287
原文地址:https://ningg.top/algorithm-series-1-summary/