AI 系列: TF-IDF 和 BM25 检索模型
2025-04-12
基本思路:
- TF-IDF 是什么含义?
- BM25 相对 TF-IDF 的改进
- 适用场景?
1. TF-IDF 是什么
TF-IDF是基于词频统计的检索算法,用于查询到最相关的文档:
- TF(Term Frequency):单个文档内,词出现的次数;次数越高,权重越大。
- IDF(Inverse Document Frequency):文档之间,包含词的文档占比(注:计算时用倒数);词在所有文档中越少见,包含这个词的文档的权重越大。
当前文档的评分:
\[score = TF \times IDF\]一次查询中,包含多个 keyword,则每个 keyword 的 score 相加,得到「当前文档」最终的 score。 score 越高,表示文档越相关。
其得分 score ,本质是「文档之间」单个文档的重要程度(
IDF)、单个文档对查询的重要程度(TF),两者叠加(相乘)。
2. BM25 对 TF-IDF 的改进
BM25是 一种经典的信息检索(IR)算法,属于 概率相关性模型(Probabilistic Relevance Model,PRM) 的一个变体。它的作用是衡量文档与查询之间的相关性,经常用在搜索引擎、推荐系统和 RAG(Retrieval Augmented Generation)等场景中。
- BM:代表 Best Matching,即“最佳匹配”。
- 25:表示这是 Okapi 系列算法(Okapi BM)中的第 25 个版本。它并不是指数学上的公式编号,而是因为在伦敦城市大学(City University, London)开发 Okapi 信息检索系统时,迭代优化了很多次,最终定稿的版本编号就是 BM25。
几个方面:
- 1.公式
- 2.细节理解
- 3.逐步算例
- 4.示例
2.1. BM25 的公式
BM25 本质是对 TF-IDF 的改进,改进点:
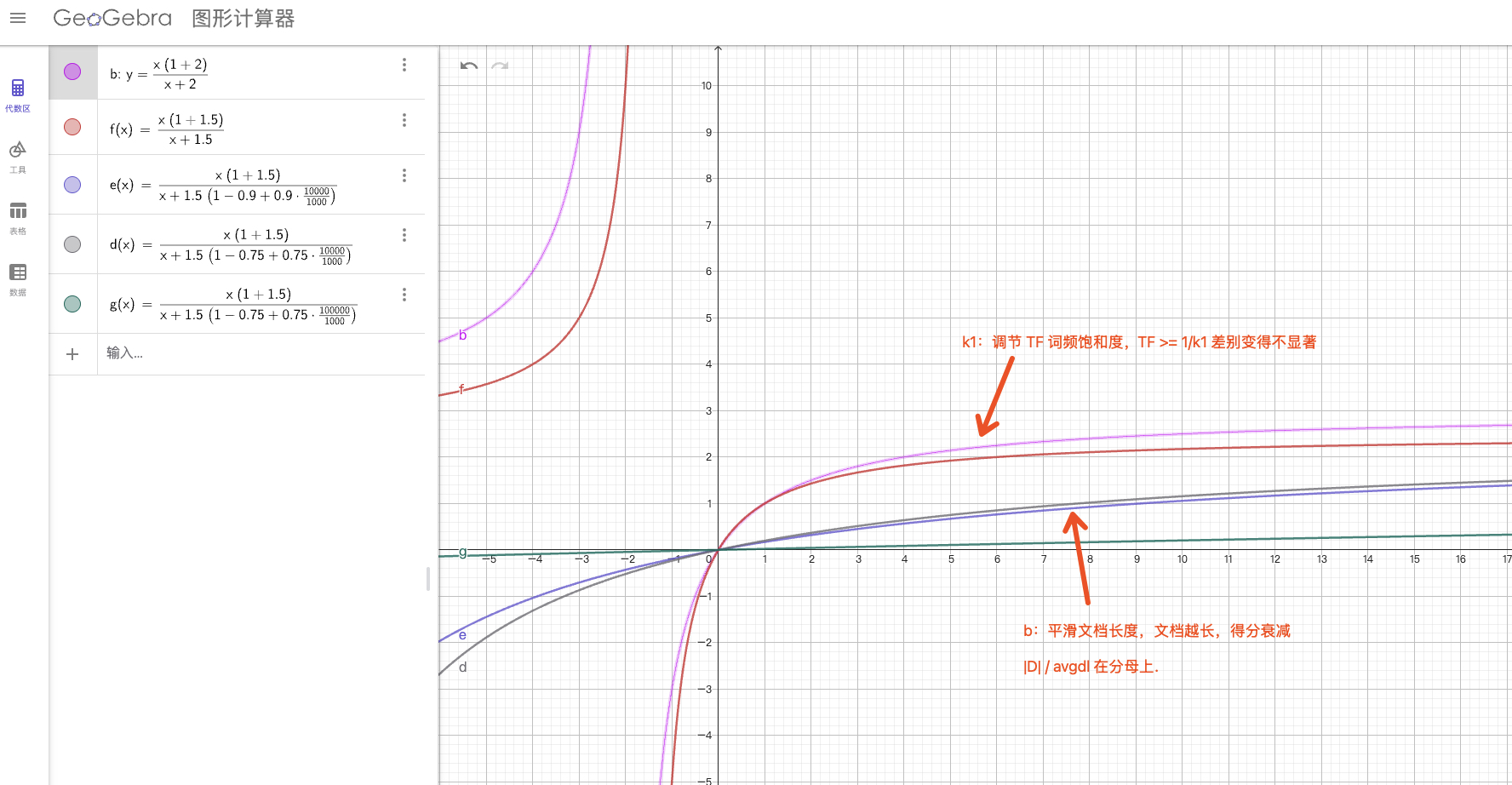
- TF 饱和:避免高词频文档无限加分(用了一个饱和函数,常见参数 k1≈1.2–2.0)。
- 文档长度归一化:避免长文档天然得分更高(参数 b≈0.75)。
- 加权公式(简化版):
对于查询 \(Q=\{q_1,q_2,\dots\}\) 与文档 \(D\),BM25 得分通常写成:
\[\text{BM25}(Q,D)=\sum_{t\in Q} \text{IDF}(t)\cdot\frac{TF(t,D)\cdot (k_1+1)}{TF(t,D) + k_1\cdot\big(1-b + b\cdot\frac{|D|}{\text{avgdl}}\big)}\]其中:
- \(TF(t,D)\):词 \(t\) 在文档 \(D\) 中的
词频(Term Frequency)。 - \(\|D\|\):文档 \(D\) 的
长度(通常用词数)。 - \(\text{avgdl}\):语料库中文档的
平均长度(average document length)。 - \(k_1\):
TF 饱和参数,控制词频上限(常见取 1.2–2.0,典型值1.5)。 - \(b\):
长度归一化强度(0 表示不做长度修正,1 表示完全按文档长度修正,常取0.75)。 - \(\text{IDF}(t)\):逆文档频率,用来衡量不同文档之间
词的区分能力(稀有词权重高)。
注:有些实现还把查询中词的频率 \(qf\) 加入,乘以一个 \(\frac{(k_3+1)qf}{k_3+qf}\) 项;但在多数实际系统里 \(qf\) 较小或当做 1,所以常被省略。
在线绘图: https://www.geogebra.org/graphing
常用的 IDF(Robertson–Sparck Jones)形式之一是:
- \(N\):语料中
文档总数。 - \(n(t)\):包含词 \(t\) 的
文档数量(Document Frequency)。 - 分子/分母各
加 0.5是平滑(避免分母为 0或极端值);再+1并取对数是为了避免出现过小或负值(有些实现不加 +1,会在 \(n> N/2\) 时得到负值)。 - 直观上:如果 \(n(t)\) 很小(词稀有),IDF 较大;如果 \(n(t)\) 很常见,IDF 小或接近 0。
2.2. 细节理解
每一项的直观解释:
- IDF(t):衡量词的区分力(包含词的文档越稀有,已经包含的文档越有用)。
- TF 部分 \(\frac{TF(k_1+1)}{TF + k_1(...)}\):
- 当 \(TF\) 很小时,得分接近线性增长;
- 当 \(TF\) 很大时,由于分母里的 \(k_1\) 项,得分趋于饱和(不会无限大)。
- 文档长度归一化 \(b\):把文档长度对得分的影响校正,避免长文档因为词更多而占优势。
- 参数意义:
- \(k_1\) 大:词频影响更显著(更少饱和)。
- \(b\) 越大:文档长度归一化越强。
2.3. 深度理解 / 注意点
- IDF 的不同写法:有些实现不加
+1或用 log base10,可能在 \(n > N/2\) 时出现负 IDF(表示该词对区分反而有负贡献),实际可根据需要平滑或截断。 - 查询词频:对长 query(或 query 中词重复)可以把 \(qf\) 也纳入,但常见短查询 \(qf=1\)。
- 参数调整:\(k_1,b\) 常通过验证集网格搜索调整;\(k_1\) 越大,词频影响越明显;\(b\) 控制长度惩罚强度。常用经验值 \(k_1\in[1.2,2.0], b\approx0.75\)。
- 停用词:对停用词(the、的)IDF 很小,贡献有限,但仍建议在检索前做停用词过滤或保留(视业务)。
- 负 IDF 情况:若使用不带 +1 的 IDF,在某些数据集上会出现负值;实现上可 clamp(截断)到 0 或使用带 +1 的变体来避免负分。
- 和向量检索混合:BM25 保留强词面精确匹配(实体、code、数字),embedding 弥补语言表达差异。常见融合:线性加权、RRF(基于排名混合)、或用 LTR(learning-to-rank)学习最优融合权重。
2.4. 示例(口头演示)
假设一个极小语料库(便于人工计算):
- 语料库有 \(N=3\) 篇文档:
- D1:
the cat sat on the mat→ 长度 \(\|D1\|=6\),词频:cat=1, hat=0 - D2:
the quick brown fox→ \(\|D2\|=4\),词频:cat=0, hat=0 - D3:
the cat and the hat→ \(\|D3\|=5\),词频:cat=1, hat=1
- D1:
- 查询 \(Q=\)
"cat hat"(两个词都在 query 中)
先计算全局量:
- N = 3
- 文档平均长度: \(\text{avgdl} = \frac{6 + 4 + 5}{3} = \frac{15}{3} = 5.0\)
- 统计 document frequency:
- \(n(\text{cat}) = 2\)(D1、D3 包含 cat)
- \(n(\text{hat}) = 1\)(仅 D3 包含 hat)
我们采用上面带 +1 的 IDF 形式:
\[\text{IDF}(t)=\ln\!\Big(\frac{N-n(t)+0.5}{n(t)+0.5}+1\Big)\]- 计算 \(\text{IDF}(\text{cat})\):
- \[\frac{N-n+0.5}{n+0.5} = \frac{3-2+0.5}{2+0.5} = \frac{1.5}{2.5} = 0.6\]
- \[0.6 + 1 = 1.6\]
- \[\text{IDF}(\text{cat}) = \ln(1.6) \approx 0.4700036293\]
- 计算 \(\text{IDF}(\text{hat})\):
- \[\frac{3-1+0.5}{1+0.5} = \frac{2.5}{1.5} \approx 1.6666666667\]
- \[1.6666666667 + 1 = 2.6666666667\]
- \[\text{IDF}(\text{hat}) = \ln(2.6666666667) \approx 0.9808292530\]
参数取常见默认:\(k_1=1.5,\; b=0.75\)。
现在对每个文档、每个 query 词计算 BM25 项(注意:若某词在文档中出现次数为 0,对应项为 0):
先把公式内的分母写成便于计算的形式(当 \(f=1\) 时):
\[\text{denom} = f + k_1\cdot\big(1-b + b\cdot\frac{|D|}{\text{avgdl}}\big)\]代入 \(k_1=1.5,\; b=0.75,\; \text{avgdl}=5\),整理一下
\[1-b = 0.25,\quad \frac{b}{\text{avgdl}} = \frac{0.75}{5} = 0.15\]所以
\[\text{denom} = 1 + 1.5\cdot(0.25 + 0.15\cdot |D|)\]分子(当 \(f=1\))是 \(f\cdot(k_1+1)=1\cdot(1.5+1)=2.5\)。
逐个文档计算(只列出 \(f=1\) 的情况):
- D1( |D1|=6):
- \[0.25 + 0.15\cdot6 = 0.25 + 0.9 = 1.15\]
- \[1.5 \cdot 1.15 = 1.725\]
- \[\text{denom} = 1 + 1.725 = 2.725\]
- 分数因子 = \(2.5 / 2.725 \approx 0.9174311927\)
- 对于词
cat(在 D1 中 \(f=1\)):项得分 \(\text{IDF(cat)} \times 0.9174311927 \approx 0.4700036293 \times 0.9174311927 \approx 0.4311959901\) - 对于词
hat:D1 中 \(f=0\) → 贡献 0。 - D1 总分 ≈ 0.4312
- D2( |D2|=4):
- \[0.25 + 0.15\cdot4 = 0.25 + 0.6 = 0.85\]
- \[1.5 \cdot 0.85 = 1.275\]
- \[\text{denom} = 1 + 1.275 = 2.275\]
- 分数因子 = \(2.5 / 2.275 \approx 1.0989010989\)
- 但 D2 中
cat和hat的 \(f=0\),所以 两项均为 0。 - D2 总分 = 0
- D3( |D3|=5):
- \[0.25 + 0.15\cdot5 = 0.25 + 0.75 = 1.0\]
- \[1.5 \cdot 1.0 = 1.5\]
- \[\text{denom} = 1 + 1.5 = 2.5\]
- 分数因子 = \(2.5 / 2.5 = 1.0\)
- 对
cat(f=1):项得分 = \(\text{IDF(cat)} \times 1.0 \approx 0.4700036293\) - 对
hat(f=1):项得分 = \(\text{IDF(hat)} \times 1.0 \approx 0.9808292530\) - D3 总分 = 0.4700036293 + 0.9808292530 ≈ 1.4508328823
最终排序(按 BM25 得分从高到低):
- D3 ≈ 1.4508
- D1 ≈ 0.4312
- D2 = 0
这与直觉一致:D3 同时包含 cat 和 hat,得分最高;D1 只含 cat;D2 什么都不含。
2.5. 总结(一句话)
BM25 = IDF(文档重要性) × TF-saturation(词频收益递减) × 长度归一化(避免长文档虚高),是一个稳健、无需训练的关键词检索基线,和 embedding 混用可以兼顾精确匹配与语义召回。
3. BM25 + Embedding 混合检索
3.1. 为什么 BM25 有效果?
从 统计角度 解释: 文档重要性 x 词频收益递减(相乘/相加) x 文档长度权重修正
- 稀有词更重要:
IDF放大,区分度高。 - 高频词饱和:常见词(比如“the”,“的”)即便出现很多次,权重不会无限增加;也可以将其列入
停用词。 - 文档长度修正:防止长文档因为字多而匹配到更多词而“虚高”。
换句话说,BM25 是一个非常稳健的文本匹配基线方法,在信息检索领域被验证了几十年。
3.2. 为什么要 BM25 + Embedding 混合检索?
- BM25 的优势:
- 擅长处理 关键词精确匹配(特别是
实体、专有名词、缩写等)。 - 无需训练,计算快。
- 擅长处理 关键词精确匹配(特别是
- Embedding 的优势:
- 能捕捉 语义相似度,即便 query 和文档用的是不同词汇(比如 “car” vs “automobile”)。
- 对自然语言问答、语义扩展友好。
- 混合检索的好处:
- BM25 保证了 词面匹配的准确性(recall)。
- Embedding 保证了 语义覆盖和泛化。
- 组合方式常见:
- 加权融合(BM25 分数归一化 + Embedding 相似度
按比例加权)。 - RRF(Reciprocal Rank Fusion):只看
排序位置而不是分数。
- 加权融合(BM25 分数归一化 + Embedding 相似度
3.3. 典型问题
- Q: “如果只用 Embedding,不用 BM25,会发生什么?”
- A: 可能会
漏掉那些 只靠词面匹配才能找到 的文档,比如专有名词、数字、代码等。
- A: 可能会
- Q: “BM25 的 IDF 为什么是 log 形式?”
- A: log 能
平滑词频分布,避免低频词权重过高,数值也更稳定。
- A: log 能
- Q: “在 RAG 系统里,BM25+Embedding 的混合是怎么调参的?”
- A: 一般通过
验证集调整 BM25 分数和 Embedding 分数的权重,或者用 学习排序(Learning-to-Rank) 自动学习最优融合方式。
- A: 一般通过
原文地址:https://ningg.top/ai-series-bm25-and-tf-idf-intro/