NingG +

动手构建大模型：阅读笔记

2025-08-02

0.背景

本文是阅读 《Build a Large Language Model 》 的笔记，记录下自己的理解。

过去一段时间关注 AI ，陆续把读研时的习惯捡回来，记录下学习过程。

先多遍阅读、每次覆盖不同要点，并结合手动操作，完全就是读研时学习前沿论文的方式，珍惜这种专注。

现在想起来，自己应该是享受类似的专注感觉：

关联术语：

1. LLM 主体流程

几个主要步骤：

其中，涉及 2 类数据：

GPT 这样的解码器模型，是通过逐字预测生成文本，因此它们被视为一种自回归模型。

[!NOTE]

自回归，是一种用于时间序列分析的统计技术，它假设时间序列的当前值是其过去值的函数。

自回归模型，使用类似的数学技术来确定序列中，元素之间的概率相关性。然后，它们使用所得知识，来猜测未知序列中的下一个元素。

自相关，用于衡量序列中元素之间的相关性；一般会圈定一个时间窗口，计算窗口内元素之间的相关性。大部分场景下，窗口之前的元素，对窗口之后的元素影响较小。

2. 数据准备

数据准备，前期处理：

Tips: 尽可能保持文本原样，仅对明确的错误进行调整。

例如： 无需将所有文本转换为小写字母，因为大写字母有助于 LLM 区分专有名词和普通名词，理解句子结构，并学习生成正确的大写文本。

数据送入模型训练之前，需要进行 分词 和 编码，得到 token 序列。

[!TIP]

BPE（Byte Pair Encoding）是 一种子词分词算法，在 NLP 领域广泛用于词表构建和文本 > tokenization（GPT、BERT 等模型中用到的就是类似方法）。它的核心思想是：通过统计频繁出现的字符对（byte pair），逐步合并成新的子词单元，从而得到一个紧凑又高效的词表。

下面详细描述 BPE 的过程：

一、BPE 的步骤

  1. 准备训练语料
    • 输入是一大段训练文本。
    • 最初，把所有单词拆成 字符序列（通常还会在单词末尾加特殊分隔符，比如 _ 或 </w> 来表示单词结束）。

    • 例如：

      "low", "lower", "newest", "widest"

      初始拆分为：

      l o w </w>
l o w e r </w>
n e w e s t </w>
w i d e s t </w>

  2. 统计字符对频率

    • 遍历所有词序列，统计相邻 字符对（pair） 的频率。
    • 例如上面数据中，最常见的 pair 可能是 ('l', 'o') 或 ('e', 's')。

  3. 合并出现频率最高的符号对

    • 找出频率最高的符号对，把它们合并成一个新的单元（子词）。
    • 例如合并 ('l', 'o') → lo，之后所有出现 "l o" 的地方都替换成 "lo"。

  4. 重复迭代

    • 不断重复步骤 2 和步骤 3，每次合并一个最频繁的 pair。
    • 每次合并后，词表中会增加一个新的子词单元（token）。

    • 例如迭代过程可能是：

      l o w </w>  → lo w </w>
lo w </w>   → low </w>

      最后可能得到 low、er、est、wid、new 这样的子词。

  5. 停止条件
    • 当达到预设的 词表大小（vocabulary size） 或迭代次数时，停止合并。
    • 最终得到的就是一个既能覆盖训练语料，又能较好泛化到新词的 子词词表。

二、BPE 的特点

  • 优点：
    • 可以处理溢出词表词（OOV），比如，新词可以拆解为已知子词组合。
    • 词表规模可控，比逐字符分割更高效，比逐词分割泛化更好。

  • 缺点：

    • 合并规则依赖于语料，可能产生一些不直观的子词切分（比如 ing 可能被拆成 in g）。
    • 对语言学结构没有显式建模，只是基于频率的统计方法。

嵌入之前，数据处理步骤：

  1. 分词：将文本拆分成单词或子词单元， 词元 又称 token ；
  2. 编码：将分词后的 token 转换为数字 ID， tokenID ；
  3. 嵌入：将 tokenID 转换为 嵌入向量（稠密向量），用于后续的模型计算。
    • 嵌入层，本质上是一个查找功能，用 token ID 作为行索引，从嵌入层的权重矩阵中检索对应行数据。
    • 除了 嵌入向量，还需要包括 位置编码，用于表示文本的顺序信息。

分词时，需要考虑 OOV 问题，即 Out of Vocabulary，即模型未见过的词汇。常见解决办法：

对于GPT类大语言模型（LLM）来说，连续向量表示（Embedding）非常重要，原因在于这些模型使用深度神经网络结构，并通过反向传播算法（back propagation）进行训练。

[!TIP]

为什么训练大语言模型（LLM）时必须有 Embedding 层？

关键在于：反向传播只能处理 数值向量，而原始文本是 离散符号。

1.离散符号无法直接参与梯度下降

  • 训练 LLM 的目标是最小化损失函数（比如交叉熵），通过 反向传播 + 梯度下降 更新参数。
  • 但文本输入是 token（单词、子词、字符）ID，比如 "apple" → 12345。
  • 这些整数 ID 是 离散的、无序的标签，它们之间没有可导关系。
    • ID=5 和 ID=6 之间没有“相近”的含义。
    • 如果直接把 token ID 喂进神经网络，梯度对输入 ID 不可导 → 无法更新参数。

2.Embedding 层的作用

Embedding 层本质是一个 可学习的查找表（矩阵），把离散 tokenID 映射成 连续向量空间的点：

  • 假设词表大小是 V，embedding 维度是 d。
  • Embedding 层参数就是一个 V × d 的矩阵 E。
  • 输入 tokenID i → 查表得到第 i 行向量 E[i] ∈ ℝ^d。

这样：

  • Token 变成了 实数向量，可以输入 Transformer 的注意力、前馈层。
  • Embedding 矩阵是 可训练参数，可以通过反向传播更新，使得相似 token 的向量逐渐靠近（语义空间逐渐形成）。

3.为什么必须有 Embedding 才能训练？

  • 从数学角度：没有 embedding，就只能把 token 当作整数，而梯度对整数不可导，训练停滞。
  • 从表示角度：Embedding 提供了一个 连续向量空间，使得离散语言符号能够以“可学习”的方式进入神经网络。
  • 从效率角度：相比 one-hot（V 维向量），embedding 把 token 压缩成 d 维，极大减少计算量。

4.类比

  • One-hot 编码：每个单词是一个超高维稀疏向量（梯度可传，但计算开销大）。
  • Embedding：相当于在训练开始时初始化一张“地图”，每个单词先随机放置在某个坐标，训练过程中逐渐移动到更合理的位置。
  • 没有 embedding：就像训练时只有“单词编号”，网络无法理解“编号之间的关系”，梯度也传不进去。

5.总结：

训练大语言模型必须有 Embedding，因为它是连接 离散符号空间 和 连续向量空间 的桥梁，使得反向传播和梯度下降能够在语言数据上发挥作用。

更多信息，参考：AI 系列：反向传播 & 梯度下降

3. 关键原理

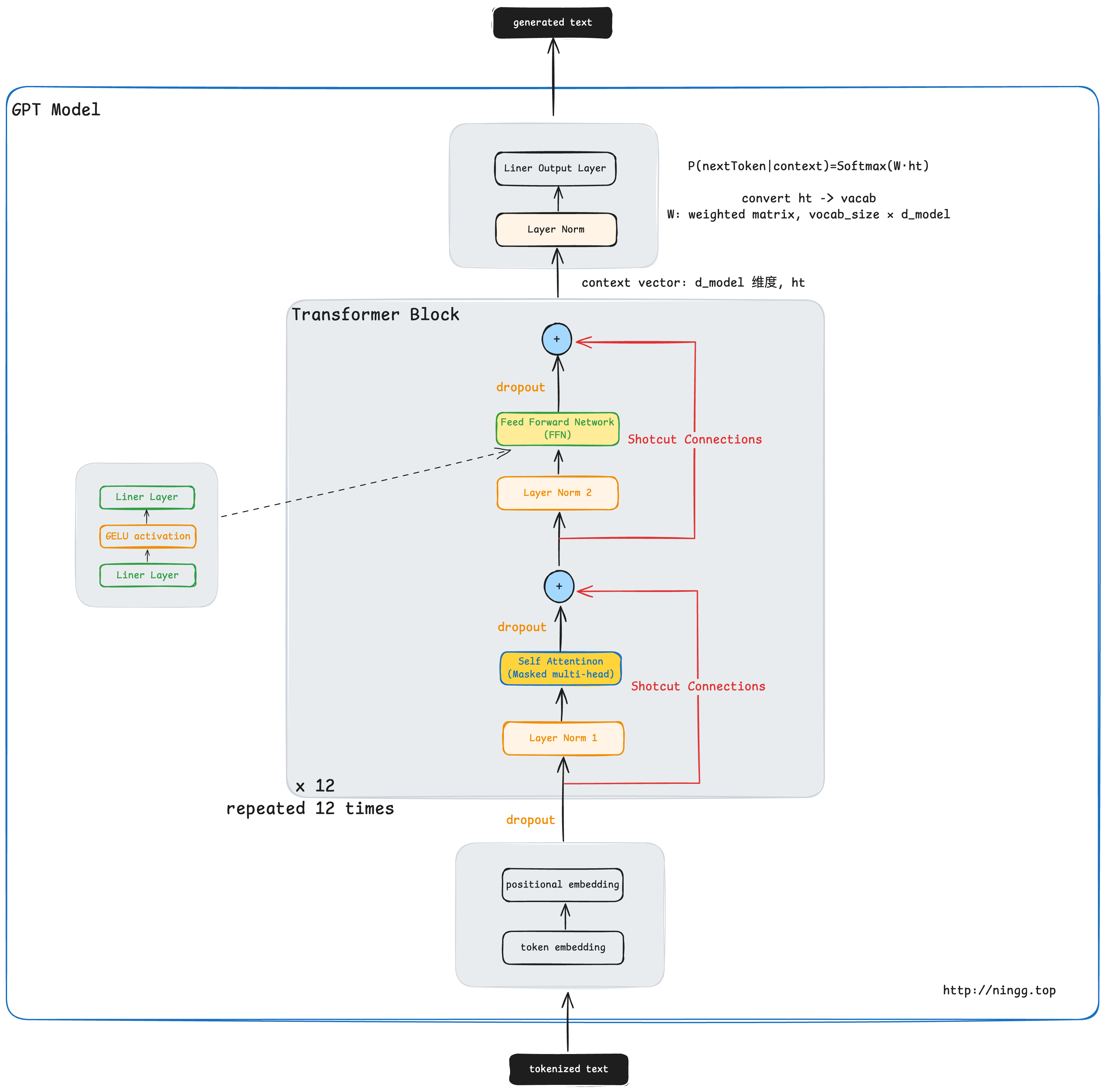
3.1. 注意力机制

编码器-解码器架构的 RNN 循环神经网络的工作原理，关键思想在于：

  1. 编码器 Encoder，将整个输入文本，处理为一个隐藏状态（记忆单元）。
  2. 解码器 Decoder，使用该隐藏状态生成输出，隐藏状态视为一个嵌入向量，它捕获了输入文本的语义信息。

RNN 的限制在于：

更多 RNN 细节：AI 系列：RNN 循环神经网络

[!TIP]

个人思考： 了解从RNN到注意力机制的技术变迁对于核心内容的理解至关重要。让我们通过一个具体的示例来理解这种技术变迁：

  1. RNN的局限性

    假设我们有一个长句子：“The cat, who was sitting on the windowsill, jumped down because it saw a bird flying outside the window.”

    假设任务是预测句子最后的内容，即要理解“it”指的是“the cat”而不是“the windowsill”或其他内容。对于 RNN 来说，这个任务是有难度的，原因如下：

    • 长距离依赖问题：在 RNN 中，每个新输入的词会被依次传递到下一个时间步。随着句子长度增加，模型的隐状态会不断被更新，但早期信息（如“the cat”）会在层层传播中逐渐消失。因此，模型可能无法在“it”出现时有效地记住“the cat”是“it”的指代对象。
    • 梯度消失问题：RNN 在反向传播中的梯度会随着时间步的增加逐渐减小，这种“梯度消失”使得模型很难在长句中保持信息的准确传播，从而难以捕捉到长距离的语义关联。

  2. 注意力机制的解决方法

    为了弥补 RNN 的这些不足，注意力机制被引入。它的关键思想是在处理每个词时，不仅依赖于最后的隐藏状态，而是允许模型直接关注序列中的所有词。这样，即使是较远的词也能在模型计算当前词的语义时直接参与。

    在上例中，注意力机制如何帮助模型理解“it”指代“the cat”呢？

    • 注意力机制的工作原理：当模型处理“it”时，注意力机制会将“it”与整个句子中的其他词进行相似度计算，判断“it”应该关注哪些词。
      • 由于“the cat”与“it”在语义上更相关，注意力机制会为“the cat”分配较高的权重，而其他词（如“windowsill”或“down”）则获得较低的权重。
    • 信息的直接引用：通过注意力机制，模型可以跳过中间步骤，直接将“it”与“the cat”关联，而不需要依赖所有的中间隐藏状态。

  3. 示例中的注意力矩阵

    假设使用一个简单的注意力矩阵，模型在处理“it”时，给每个词的权重可能如下（至于如何计算这些权重值后文会详细介绍）：

    词 The cat who was sitting … it saw bird flying … window
    权重 0.1 0.3 0.05 0.05 0.05 … 0.4 0.05 0.02 0.01 … 0.02

    在这个注意力矩阵中，可以看到“it”对“the cat”有较高的关注权重（0.3），而对其他词的关注权重较低。这种直接的关注能力让模型能够高效捕捉长距离依赖关系，理解“it”与“the cat”的语义关联。

自注意力机制，是一种允许输入序列中的每个位置都能与同一序列中所有位置进行交互，并权衡他们的重要性。

在自注意力机制中，我们的目标是：

[!TIP]

个人思考： 这里对于注意力得分的计算描述的比较笼统，仅仅说明了将当前的输入Token向量与其它Token的向量进行点积运算计算注意力得分，实际上，每个输入Token会先通过权重矩阵W分别计算出它的Q、K、V三个向量，这三个向量的定义如下：

  • Q向量（查询向量）：查询向量代表了这个词在寻找相关信息时提出的问题
  • K向量（键向量）：键向量代表了一个单词的特征，或者说是这个单词如何”展示”自己，以便其它单词可以与它进行匹配
  • V向量（值向量）：值向量携带的是这个单词的具体信息，也就是当一个单词被”注意到”时，它提供给关注者的内容

更通俗的理解： 想象我们在图书馆寻找一本书（Q向量），我们知道要找的主题（Q向量），于是查询目录（K向量），目录告诉我哪本书涉及这个主题，最终我找到这本书并阅读内容（V向量），获取了我需要的信息。

具体生成Q、K、V向量的方式主要通过线性变换：

Q1 = W_Q * (E1 + Pos1)
K1 = W_K * (E1 + Pos1)
V1 = W_V * (E1 + Pos1)

依次类推，为所有token生成Q，K，V向量，其中W_Q，W_K和W_V是Transformer训练出的权重（每一层不同）

针对每一个目标token，Transformer会计算它的 Q向量 与其它所有的token的 K向量 的点积，以确定每个词对当前词的重要性（即注意力分数）

假如有句子：“The cat drank the milk because it was hungry”

例如对于词 cat 的 Q向量 Q_cat，模型会计算：

  • score_cat_the = Q_cat · K_the — 与the的语义相关度
  • score_cat_drank = Q_cat · K_drank — 与 drank 的语义相关度
  • score_cat_it = Q_cat · K_it — 与 it 的语义相关度
  • 依此类推，得到cat与句子中其它所有token的注意力分数 [score_cat_the、score_cat_drank、socre_cat_it、……]

计算上下文向量前，会对权重归一化，将注意力得分、转换为注意力权重：一般用 softmax 函数。

理解点积

点积运算本质上是一种将两个向量按元素相乘后再求和的简单方式，我们可以如下演示：

res = 0.
for idx, element in enumerate(inputs[0]):
     res += inputs[0][idx] * query[idx]
print(res)
print(torch.dot(inputs[0], query))

输出结果确认，逐元素相乘的和与点积的结果相同。

tensor(0.9544)
tensor(0.9544)

除了将点积运算视为结合两个向量并产生标量结果的数学工具之外，点积也是一种相似度的衡量方法，因为它量化了两个向量的对齐程度：较高的点积值表示向量之间有更高的对齐程度或相似度。在自注意力机制的背景下，点积决定了序列中元素之间的关注程度：点积值越高，两个元素之间的相似度和注意力得分就越高。

[!TIP]

个人思考： 这里稍微延伸探讨一下Softmax, 它是一种常用的激活函数，尤其在神经网络的分类任务中被广泛使用。它的作用是将一个任意的实数向量转换为一个概率分布，且所有元素的概率之和为 1。下面通过例子来说明 softmax 的原理、好处，以及它在神经网络中的使用原因。

  1. Softmax 的原理

    Softmax 函数的公式如下：

    \[\text{softmax}\left(z_{i}\right)=\frac{e^{z_{i}}}{\sum_{j} e^{z_{j}}}\]

    其中 \(z_{i}\) 是输入的每个分数（即未激活的原始值），e 是自然对数的底。这个公式的作用是将输入向量中的每个元素转换为一个概率值，且所有值的和为 1。

  2. Softmax 的好处

    • 归一化输出为概率：Softmax 将输出转换为 0 到 1 之间的概率，且所有类别的概率之和为 1，方便解释结果。例如，在分类任务中，输出可以直接表示模型对各类别的信心。
    • 平滑和放大效果：Softmax 不仅能归一化，还具有平滑和放大效果。较大的输入值会被放大，较小的输入值会被抑制，从而增强模型对最优类别的区分。
    • 支持多分类问题：与 sigmoid 不同，Softmax 适用于多类别分类问题。它可以输出每个类别的概率，使得模型可以处理多分类任务。

  3. 神经网络为什么喜欢使用 Softmax

    在神经网络中，特别是分类模型（如图像分类、文本分类）中，Softmax 层通常用作最后一层输出。原因包括：

    • 便于优化：在分类任务中，Softmax 输出的概率分布可与真实的标签概率进行比较，从而计算交叉熵损失。交叉熵损失的梯度较为稳定，便于模型的优化。
    • 概率解释：Softmax 输出可以解释为“模型对每个类别的信心”，使得输出直观可理解。
    • 与交叉熵的结合：Softmax 与交叉熵损失函数结合效果特别好，可以直接将模型预测的概率分布与真实标签比较，从而更快收敛，效果更好。

  4. 激活函数

    激活函数（Activation Function）是神经网络中的核心组件，它的作用类似于神经元的“开关”或“过滤器”，负责决定神经元是否被激活（即输出信号），以及激活的程度。

    在神经网络中，激活函数通常用于将输入信号转换为输出信号，从而实现非线性变换。 常见的激活函数包括：

    • Sigmoid：将输入信号转换为0到1之间的概率值，常用于二分类问题。
    • ReLU：将输入信号转换为0到正无穷之间的值，常用于多分类问题。
    • Softmax：将输入信号转换为0到1之间的概率值，常用于多分类问题。

3.2. 上下文向量

疑问：llm 大模型的自注意力机制中，每个输入 token 对应的上下文向量，有什么作用？被用于做什么？

在 LLM 大模型的自注意力机制 (Self-Attention) 里，每个输入 token（词或子词）在计算时，都会得到一个 上下文向量（context vector）。

1. 上下文向量是怎么来的？

在自注意力里：

换句话说：

上下文向量 = 当前 token 从其他 token 那里「聚合」来的信息。

2. 上下文向量的作用

上下文向量不是终点，而是 后续计算的输入，主要用在以下方面：

a. 更新 token 表示

b. 为下一层提供输入

c. 用于预测下一个 token（解码阶段）

3. 可以打个比喻

4.总结一句话

在 LLM 的自注意力里，每个输入 token 的上下文向量，起到“把自己和全局上下文融合”的作用，既用于更新 token 的表示，也直接服务于最后的下一个 token 预测。

3.3. 缩放：注意力得分

缩放注意力得分：通过将注意力得分除以keys嵌入维度的平方根来进行缩放（注意，取平方根在数学上等同于指数为 0.5 的运算）。再使用 softmax 函数来计算注意力权重。

[!NOTE]

缩放点积注意力机制的原理

对嵌入维度大小进行归一化的原因是为了避免出现小梯度，从而提高训练性能。例如，当嵌入维度增大时（在 GPT 类大型语言模型中通常超过一千），较大的点积在反向传播中应用 softmax 函数后，可能会导致非常小的梯度。随着点积的增大，softmax 函数的行为会更加类似于阶跃函数，导致梯度接近于零。这些小梯度可能会显著减慢学习速度，甚至导致训练停滞。

通过嵌入维度的平方根进行缩放，正是自注意力机制被称为‘缩放点积注意力’的原因。

[!TIP]

个人思考： 这里再稍微解释一下上述关于缩放点积注意力的机制。在自注意力机制中，查询向量（Query）与键向量（Key）之间的点积用于计算注意力权重。然而，当嵌入维度（embedding dimension）较大时，点积的结果可能会非常大。那么大的点积对接下来的计算有哪些具体影响呢？

  • Softmax函数的特性：在计算注意力权重时，点积结果会通过Softmax函数转换为概率分布。而Softmax函数对输入值的差异非常敏感，当输入值较大时，Softmax的输出会趋近于0或1，表现得类似于阶跃函数（step function）。
  • 梯度消失问题：当Softmax的输出接近0或1时，其梯度会非常小，接近于零（可以通过3.3.1小节中提到的Softmax公式推断）。这意味着在反向传播过程中，梯度更新幅度会很小，导致模型学习速度减慢，甚至训练停滞。

为了解决上述问题，在计算点积后，将结果除以嵌入维度的平方根（即 \(\sqrt{dk}\)），其中 dk 是键向量的维度。这样可以将点积结果缩放到适当的范围，避免Softmax函数进入梯度平缓区，从而保持梯度的有效性，促进模型的正常训练。

3.4. 权重矩阵 Q\K\V

疑问：llm 的注意力机制中，为什么要使用 Q/K/V 权重矩阵，只使用 Q/V 不行吗？或者，使用更多权重矩阵可以吗？

1. Q/K/V 各自的角色

在 Transformer 自注意力里，输入 token 的 embedding/隐藏向量 \(x\) 会经过 三个不同的线性变换：

然后通过公式：

\[Attention(Q, K, V) = softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]

核心逻辑：

2. 为什么不能只用 Q/V？

假设只用 Q 和 V（没有 K）：

所以，K 的存在提供了一个 抽象的匹配空间，让 Q 可以快速决定该关注哪些 V。

3. 能不能用更多的权重矩阵？

可以，但不一定有意义。

实际上，学术界确实有一些扩展版本：

4. 总结

5. 类比图

类比图（图书馆：读者需求=Q，书标签=K，书内容=V），让你更直观地理解为什么 K 不能省？

3.5. dropout 剪枝(随机丢弃)

Dropout 在深度学习中是一种技术，即在训练过程中随机忽略一些隐藏层单元，实际上将它们“丢弃”。这种方法有助于防止过拟合 overfitting，确保模型不会过于依赖任何特定的隐藏层单元组合，提升泛化能力。需要特别强调的是，Dropout 仅在训练过程中使用，训练结束后则会禁用。

在 Transformer 架构中（包括 GPT 等模型），注意力机制中的 Dropout 通常应用于两个特定区域：计算注意力得分之后，或将注意力权重应用于 value 向量之后。具体位置：在大语言模型中（如 Transformer 结构里），dropout 通常出现在以下位置：

  1. Embedding 层之后
  2. Self-Attention 输出后
  3. Feed-Forward 层输出后

[!TIP]

个人思考： Dropout相当于丢弃一定比例的注意力权重，这表明对输入中的某些token关注度降为0了（完全不关注），这样的处理方式难道对最终的预测效果没有影响么？另外如何理解Dropout之后的缩放操作是为了保持注意力在不同阶段的平衡？

经过查阅额外的资料及深度思考，我觉得可以从以下几个方面理解上述的疑问：

  1. Dropout 的目的：提高模型的泛化能力

    dropout 的设计初衷是提高模型的泛化能力。通过随机丢弃一部分神经元或注意力权重，dropout 迫使模型在每次训练时学习略有不同的表示方式，而不是依赖某一特定的注意力模式。这种随机化的训练方式可以帮助模型在面对新数据时更具鲁棒性，减少过拟合的风险。

  2. 注意力机制的冗余性

    在 Transformer 的注意力机制中，模型通常会对多个 token 进行注意力计算，实际上会有一些冗余信息。也就是说，不同 token 之间的信息通常会有部分重叠，并且模型能够从多个来源获取类似的信息。在这种情况下，dropout 随机丢弃一部分注意力权重并不会完全破坏模型的性能，因为模型可以依赖于其他未被丢弃的注意力路径来获取所需信息。

  3. 缩放操作的作用

    在应用 dropout 时，一部分注意力权重被随机置零（假设 dropout 率为 p）。剩余的权重会被放大，其放大倍数为 \(\frac{1}{1-p}\)。放大后的权重记为 z′：

    \[z_{i}^{\prime}=\frac{z_{i}}{1-p} \quad \text { (对于未被置零的权重) }\]

    此时，未被置零的注意力权重 \(\mathbf{z}'\) 将作为 Softmax 的输入。因此，dropout 后的缩放对 Softmax 有两个主要影响：

    • 增大未遮盖值的相对差异：放大剩余权重后，它们的数值相对于被置零的权重增大，从而拉大了非零元素之间的相对差异。这使得在 Softmax 计算中（通过前文提过的Softmax公式推导，输入值的差异越大，输出分布就会越尖锐；而输入值差异越小，输出分布就会越平滑），剩下的值之间的对比更明显。
    • 影响 Softmax 输出的分布形态：当未被置零的权重值被放大后，它们在 Softmax 输出中会更具代表性，注意力分布会更集中（即更尖锐），让模型更关注特定的 token。

    缩放后的 Softmax 输入导致注意力分布更倾向于少数的高权重 token，使得模型在当前步骤更关注这些 token 的信息。这对模型的影响包括：

    • 增强模型的选择性关注：在训练中，模型会在每个步骤中随机选择不同的 token 进行更高的关注，这使模型在学习时不会依赖特定 token 的注意力。
    • 确保总注意力强度保持一致：即便经过 dropout 丢弃了一部分权重，缩放保证了剩余权重在 Softmax 后的分布与未应用 dropout 时类似。

  4. 训练过程中多次迭代弥补信息丢失

在训练过程中，每个 batch 中的 dropout 掩码都是随机生成的。也就是说，在每次训练时被丢弃的注意力权重是随机的，并不会始终忽略相同的 token。这种随机性确保了在训练过程中，模型会在多个迭代中多次关注到每个 token。因此，即便某个 token 在当前的训练步中被忽略，在未来的训练步骤中它仍然会被关注到，从而在整体上避免了信息丢失的问题。

3.6. 层归一化

层归一化，以提高神经网络训练的稳定性和效率。

归一化的核心思想：将神经网络层的激活（输出）调整为均值=0，方差=1（即单位方差），即 正态分布

1. LayerNorm 含义

在一个神经网络层的输出中，每个Token的 特征向量（通常是隐藏层维度 (d) 的向量）都会做一次归一化。

其做法是：对某一层输出的 同一个 Token 的所有特征维度 进行均值和方差的标准化处理。

公式如下： 均值为0、方差为1的正态分布 (减均值、除方差)

\[\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\]

其中：

接着会引入两个可学习的参数：缩放系数 \(\gamma\) 和偏移量 \(\beta\)，得到最终输出：

\[y_i = \gamma \hat{x}_i + \beta\]

2.在 Transformer/LLM 中的作用

在 LLM（如 GPT）中，每个 Transformer Block 里都会使用 LayerNorm：

  1. 保证不同层、不同 token 的表示分布稳定，避免梯度爆炸或消失。
  2. 在训练中加快收敛，帮助模型更好地学习。
  3. 提升模型在大规模参数情况下的数值稳定性。

常见的使用方式有两种：

现在主流，全部是前置LayerNorm。

[Note]:

1.前置 Pre-LayerNorm，结构如下：(子层和残差是连续的，LayerNorm 在前/在后)

x -> LayerNorm -> Sublayer (Attention/FFN) -> Add(Residual) -> Output
  • 即：在进入子层之前，先做 LayerNorm，再走注意力或 FFN，然后残差加回。
  • 优点：
    • 更稳定，特别是当层数很深时（几十层甚至上百层的 GPT、LLaMA 等）。
    • 保持梯度流通，梯度更容易传递到前面层，避免训练早期梯度消失。
  • 缺点：模型的表示在推理时有时不如 Post-LN 那么「干净」，但整体可控。

2.后置 Post-LayerNorm，结构如下：

x -> Sublayer (Attention/FFN) -> Add(Residual) -> LayerNorm -> Output
  • 也就是说：先经过子层（Self-Attention 或 FFN），再加上残差，最后做 LayerNorm。
  • 优点：结构直观，最早的 Transformer 论文就是这样。
  • 缺点：训练深层网络时不稳定（梯度容易消失/爆炸）。

此外，补充一点 梯度消失、梯度爆炸信息：

a.梯度消失（Vanishing Gradients）
b.梯度爆炸（Exploding Gradients）
c.二者的关系
d.是否会同时发生？
e.应对方法
f.总结一句

3.和 BatchNorm 的区别

因此：

3.7. 前馈神经网络 FFN

FeedForward 模块是一个小型神经网络，由两个线性层和一个 GELU 激活函数组成。

FeedForward 模块对模型能力的增强（主要体现在从数据中学习模式并泛化方面）起到了关键作用。尽管该模块的输入和输出维度相同，但在内部，它首先通过第一个线性层将嵌入维度扩展到一个更高维度的空间（如上图所示）。之后再接入非线性 GELU 激活，最后再通过第二个线性层变换回原始维度。这样的设计能够探索更丰富的表示空间。

[!TIP]

个人思考： 这段描述一笔带过了扩展和收缩嵌入维度为模型训练带来的好处，那到底该如何理解这样的设计能够探索更丰富的表示空间呢？

可以将扩展和收缩的过程类比为一种数据解压缩与重新压缩的机制：

  • 扩展（解压缩）：假设我们有一段压缩的音乐文件（例如 MP3），里面包含了音频的基本信息。通过解压缩（扩展），我们把这个文件变成了一个更高质量的音频格式，允许我们看到（听到）更多的细节，比如乐器的细微声响和音调变化。
  • 特征提取：接着，我们可以在这个高质量的音频文件中应用各种音频处理算法（相当于非线性激活），分析出更多细节，比如每种乐器的声音特点。
  • 收缩（压缩）：最后，我们将音频再次压缩为一种更适合传输和存储的格式。虽然最终文件变小了，但这个文件已经包含了之前提取出的更多的声音细节。

将这种理解再应用到神经网络中，扩展后的高维空间可以让模型“看到”输入数据中更多的隐藏特征，提取出更丰富的信息。然后在收缩回低维度时，这些丰富的特征被整合到了输入的原始维度表示中，使模型最终的输出包含更多的上下文和信息。

3.8. 残差连接

残差连接，是一种在神经网络中广泛使用的技巧，用于帮助模型训练更深层的网络：用于缓解梯度消失问题。梯度消失是指，在训练中指导权重更新的梯度在反向传播过程中逐渐减小，导致早期层（靠近输入端的网络层）难以有效训练。

[!TIP]

个人思考： 看到这里，不知各位读者是否真正理解了快捷连接在深度神经网络中的作用，这里其实涉及到快捷连接的两个重要的作用：

  • 保持信息（或者说是特征）流畅传递
  • 缓解梯度消失问题

让我们逐一解读，LLM 中的每个Transformer 模块通常包含两个重要组件（可以先阅读完4.5节，再回头看这里的解读）：

  1. 自注意力层（Self-Attention Layer）：计算每个 token 与其他 token 的关联，帮助模型理解上下文。
  2. 前馈网络（Feed Forward Network）：对每个 token 的嵌入（embedding）进行进一步的非线性转换，使模型能够提取更复杂的特征。

这两个部分都在层归一化（Layer Normalization）和快捷连接（Shortcut Connections）的配合下工作。

假设我们正在训练一个 LLM ，并希望它理解下面的句子：

The cat sat on the mat because it was tired.

模型需要通过多个 Transformer 层来逐层处理该句子，使得每个词（token）在上下文中能被理解。为了达到这一目的，每个 token 的嵌入会在多层中进行注意力计算和前馈网络处理。

  1. 没有快捷连接时的情况

    如果没有快捷连接，那么每个 Transformer 层的输出就直接传递到下一个层。这种情况下，网络中的信息流大致如下：

    • 层间信息传递的局限：假设当前层的注意力机制计算出了“it”和“cat”之间的关系，如果前馈网络进一步转换了这个信息，那么下一层就只能基于该层的输出，可能丢失一些最初的语义信息。
    • 梯度消失：在训练过程中，梯度从输出层逐层向回传播。如果层数过多，梯度会逐渐变小（即“梯度消失”），从而导致模型难以有效更新前面层的参数。

    这种情况下，由于信息不能直接流动到更深层次的网络，可能会导致模型难以有效捕捉到前层的一些原始信息。

  2. 加入快捷连接后的情况

    加入快捷连接后，信息可以在层与层之间直接跳跃。例如，假设在第 n 层，我们有输入 \(X_{n}\) ，经过注意力和前馈网络得到输出 \(F(X_{n})\) 。加入快捷连接后，这一层的输出可以表示为：

    \[\text { 输出 }=X_{n}+F\left(X_{n}\right)\]

    这意味着第 n 层的输出不仅包含了这一层的新信息 \(F(X_{n})\) ，还保留了原始输入 \(X_{n}\) 的信息。下面是这样做的好处：

    • 保留原始信息

      快捷连接让输入的原始信息直接传递到后续层，避免了在多层处理过程中丢失重要信息。例如，“it” 和 “cat” 之间的关系在较浅层中被捕捉到后，即使后面的层有进一步的处理，模型依然能够从快捷连接中获得最初的上下文信息。

    • 减轻梯度消失

      假设我们有一个简单的三层网络，第三层的输出 O 是整个网络的输出。我们从损失函数 LLL 开始计算梯度：

      • 根据反向传播的原理，无快捷连接时，梯度必须逐层传递，如下：

        \[\frac{\partial L}{\partial X_{1}}=\frac{\partial L}{\partial X_{3}} \cdot \frac{\partial X_{3}}{\partial X_{2}} \cdot \frac{\partial X_{2}}{\partial X_{1}}\]

        这里，如果某一层的梯度值很小，那么梯度会被逐层缩小，导致梯度消失。

      • 有快捷连接时，假设我们在每一层之间都添加快捷连接，梯度的传播路径就多了一条直接路径：

        \[\frac{\partial L}{\partial X_{1}}=\frac{\partial L}{\partial\left(X_{1}+F\left(X_{1}\right)\right)} \cdot\left(1+\frac{\partial F\left(X_{1}\right)}{\partial X_{1}}\right)\]

        这样，即使 \(\frac{\partial F\left(X_{1}\right)}{\partial X_{1}}\) 很小，梯度依然可以通过 111 这条路径直接传递到更前面的层。

4. 核心架构

llm 架构，核心模块：

4.1. 预测下一个 token

疑问：训练 LLM 模型时，预测下一个 token 时，使用的是「上一个 token」计算出来的「注意力权重」反算出来概率最大的 token吗？

LLM 在训练时是如何预测下一个 token 的：

1. 输入是什么？

假设我们有一句话：

“I like to eat”

在训练时，模型看到的输入 token 序列是：

[I] [like] [to] [eat]

模型的任务是 预测下一个 token，也就是：

I -> like  
like -> to  
to -> eat  
eat -> <end>

2. 注意力在做什么？

3. 如何得到下一个 token 的概率？

所以，它不是直接用「注意力权重」来反推，而是： 注意力权重 → 融合得到上下文向量 → 输出层映射到词表 → Softmax 得到概率分布。

4. 训练目标

5. 总结

4.2. 交叉熵损失

模型输出的是 上下文向量，通过 输出层 + softmax 得到概率分布，再通过 交叉熵损失 计算损失，反向传播更新模型权重。

在大语言模型（LLM）的训练中，交叉熵损失（Cross-Entropy Loss）是最常用的目标函数，它衡量模型预测的概率分布与真实标签分布之间的差异。

下面从公式、直观含义和 LLM 场景的实际计算步骤三方面说明：

1. 公式

假设：

交叉熵定义：

\[H(q, p) = - \sum_{i=1}^V q_i \log p_i\]

由于 \(q\) 是 one-hot，假设目标词索引是 \(y\)，则简化为：

\[\text{Loss} = - \log p_y\]

即：取模型对 正确词 的预测概率 (\(p_y\))，取对数，再加负号，并没有求和累加。

2. 直观理解

换句话说，交叉熵损失趋近0，就是让模型 更确信正确词，不断提高它的预测概率。

3. 在 LLM 训练中的实际计算

训练一个 LLM 时，输入一段文本序列：

\[x = (w_1, w_2, w_3, \dots, w_T)\]

模型的任务是预测下一个词：

\[P(w_t \mid w_1, w_2, \dots, w_{t-1})\]

所以：

4. 与 softmax 的关系

在实现中，模型输出的是 logits（未归一化的分数）：

\[z = (z_1, z_2, \dots, z_V)\]

经过 softmax 得到概率分布：

\[p_i = \frac{e^{z_i}}{\sum_{j=1}^V e^{z_j}}\]

交叉熵损失实际计算为：

\[\text{Loss} = -z_y + \log\left(\sum_{j=1}^V e^{z_j}\right)\]

这也是深度学习框架中常见的 CrossEntropyLoss (logits, labels) 公式。

5.总结

在 LLM 中，交叉熵损失就是“对正确词预测概率的负对数”。训练目标是最大化目标序列的似然（MLE），等价于最小化交叉熵。

[!NOTE]

反向传播

如何最大化目标 token 的 softmax 概率值？整体思路是通过更新模型权重，使模型在生成目标 token 时输出更高的概率值。权重更新通过一种称为反向传播的过程来实现，这是一种训练深度神经网络的标准技术。

反向传播需要一个损失函数，该函数用于计算模型预测输出与实际目标输出之间的差异（此处指与目标 token ID 对应的概率）。这个损失函数用于衡量模型预测与目标值的偏差程度。

[!TIP]

个人思考： 在继续接下来的计算之前，我们首先来探讨一下，对数在损失函数的应用中到底有什么作用。

  1. 为什么要用概率的对数

    在 LLM 中，概率得分通常是小于1的数（例如0.1、0.05等），直接用这些数进行计算和优化可能会面临一些问题。比如，如果多个概率相乘，结果会变得非常小，甚至接近0。这种情况称为“数值下溢”（Numerical Underflow），可能导致计算不稳定。

    假设我们有三个概率值，分别为0.2、0.1和0.05。如果我们计算这些值的乘积，结果是：

    \[0.2×0.1×0.05=0.001\]

    这个值非常小，尤其在深度学习或概率模型中，我们通常会有成千上万个概率需要相乘，这样会导致最终的乘积接近0甚至为0，造成数值计算的不稳定性。

    如果我们对这些概率值取对数，然后相加，而不是直接相乘，我们可以避免这个问题。例如，对这三个值取自然对数（logarithm）后再相加：

    \[ln(0.2)+ln(0.1)+ln(0.05)≈−1.6094+(−2.3026)+(−2.9957)=−6.9077\]

    虽然这个和也是负数，但它不会像直接相乘的结果那样接近于0，避免了数值下溢的问题。对数的累加性质允许我们将原本的累乘操作转换为累加，使得计算更加稳定和高效。

  2. 对数概率在损失函数中的作用

    GPT模型训练的目标是最大化正确目标 token 的概率，通常，我们会使用交叉熵损失来衡量模型预测与实际目标之间的差异。对于一个目标 token 序列 \(y=(y1,y2,…,yn)\)，GPT会生成一个对应的预测概率分布 \(P(y∣x)\)，其中 \(x\) 是模型的输入。

    交叉熵损失的公式：

    在计算交叉熵损失时，我们希望最大化模型分配给每个正确目标token的概率。交叉熵损失的数学公式为：

    \[\text { Loss }=-\sum_{t=1}^{T} \ln P\left(y_{t} \mid x, \theta\right)\]

    其中：

    • T 是序列长度
    • \(y_{t}\) 是在位置 t 上的目标token
    • \(P(y_{t}∣x,θ)\) 是模型在参数 θ 下对目标token \(y_{t}\) 的条件概率

    在公式中，对每个token的概率 \(P(y_{t}∣x,θ)\) 取对数，将乘积形式的联合概率转换为求和形式，有助于避免数值下溢，同时简化优化过程。

[!NOTE]

交叉熵损失

本质上，交叉熵损失是在机器学习和深度学习中一种常用的度量方法，用于衡量两个概率分布之间的差异——通常是标签的真实分布（此处为数据集中的 token）和模型的预测分布（例如，LLM 生成的 token 概率）。

在机器学习，特别是 PyTorch 等框架中，cross_entropy 函数用于计算离散输出的损失，与模型生成的 token 概率下的目标 token 的负平均对数概率类似。因此，cross entropy 和负平均对数概率这两个术语在计算上有关联，实践中经常互换使用。

4.3. 交叉熵损失，实践

问题：实际训练过程中，输入的是一个 token 序列，预测的只是下一个 token，这种情况下，是不是交叉熵损失函数，就没有求和的过程？

回答：不对，也有求和。

这个问题问得很关键，确实，在实现上会让人困惑：输入的是一个 token 序列，预测下一个 token，那交叉熵损失到底有没有「求和」？

1. 理论公式

我们刚才说的 交叉熵损失是：

\[\text{Loss}(x) = - \sum_{t=1}^T \log P_\theta(w_t \mid w_{<t})\]

也就是说，对于一整段序列 \((w_1, w_2, \dots, w_T)\)，它是 逐位置（token）预测的 log 概率的求和。

如果训练时的 batch 里有多条序列，那还要对 batch 求和 / 平均。

2. 实际训练实现上

在深度学习框架（如 PyTorch）里，一般是这样做的：

  1. 输入序列：

    \[[w_1, w_2, \dots, w_T]\]

  2. 模型输出 logits： 形状是 \((T, V)\)，其中 V 是词表大小。 每一行是 softmax 前的 logit，表示「当前位置预测下一个 token」的分布。

  3. 交叉熵计算： 框架提供的 CrossEntropyLoss(logits, labels) 会：

    • 对每个位置 (t)，取目标 token (\(w_t\))，计算 \(-\log P(w_t \mid w_{<t})\)。
    • 默认会对所有位置的损失 求平均（reduction="mean"）。

3. 为什么看起来像“没有求和”？

但实际上，它内部是：

\[\text{Loss} = \frac{1}{T} \sum_{t=1}^T -\log P_\theta(w_t \mid w_{<t})\]

只是框架帮我们完成了求和 / 平均。

4. 特殊情况

5. 总结

5.实例代码

模型核心：生成 上下文向量，如下。

# Listing 4.7 The GPT model architecture implementation
class GPTModel(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"])
        self.pos_emb = nn.Embedding(cfg["context_length"], cfg["emb_dim"])
        self.drop_emb = nn.Dropout(cfg["drop_rate"])

        self.trf_blocks = nn.Sequential(
            *[TransformerBlock(cfg) for _ in range(cfg["n_layers"])])

        self.final_norm = LayerNorm(cfg["emb_dim"])
        self.out_head = nn.Linear(
            cfg["emb_dim"], cfg["vocab_size"], bias=False
        )

    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_embeds = self.tok_emb(in_idx)

        pos_embeds = self.pos_emb(torch.arange(seq_len, device=in_idx.device))      #A
        x = tok_embeds + pos_embeds
        x = self.drop_emb(x)
        x = self.trf_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

 #A 设备设置将根据输入数据所在的位置选择在 CPU 或 GPU 上训练模型

基于核心 model，实现 token 生成过程：

# Listing 4.8 A function for the GPT model to generate text
def generate_text_simple(model, idx, max_new_tokens, context_size): #A
    for _ in range(max_new_tokens):
        idx_cond = idx[:, -context_size:]                           #B
        with torch.no_grad():
           logits = model(idx_cond)

        logits = logits[:, -1, :]                                   #C
        probas = torch.softmax(logits, dim=-1)                      #D
        idx_next = torch.argmax(probas, dim=-1, keepdim=True)       #E
        idx = torch.cat((idx, idx_next), dim=1)                     #F

    return idx


#A idx 是当前上下文中索引的数组，形状为 (batch, n_tokens)
#B 若上下文长度超出支持范围，则进行裁剪。例如，若模型仅支持 5 个 token，而上下文长度为 10，仅使用最后 5 个 token 作为上下文
#C 仅关注最后一个时间步，将形状从 (batch, n_token, vocab_size) 转换为 (batch, vocab_size)
#D probas 的形状为 (batch, vocab_size)
#E idx_next 的形状为 (batch, 1)
#F 将采样的索引追加到当前序列中，此时 idx 的形状为 (batch, n_tokens+1)

工具函数，用于计算由训练和验证加载器返回的批量数据的交叉熵损失：

def calc_loss_batch(input_batch, target_batch, model, device):
    input_batch, target_batch = input_batch.to(device), target_batch.to(device)       #A
    logits = model(input_batch)
    loss = torch.nn.functional.cross_entropy(
        logits.flatten(0, 1), target_batch.flatten()
    )
    return loss

#A 将数据传输到指定设备（如 GPU），使数据能够在 GPU 上处理。

训练流程：

# Listing 5.3 The main function for pretraining LLMs
def train_model_simple(model, train_loader, val_loader, optimizer, device, num_epochs,
                       eval_freq, eval_iter, start_context, tokenizer):
    train_losses, val_losses, track_tokens_seen = [], [], []                        #A
    tokens_seen, global_step = 0, -1

    for epoch in range(num_epochs):                                                 #B
        model.train()
        for input_batch, target_batch in train_loader:
            optimizer.zero_grad()                                                   #C
            loss = calc_loss_batch(input_batch, target_batch, model, device)
            loss.backward()                                                         #D
            optimizer.step()                                                        #E
            tokens_seen += input_batch.numel()
            global_step += 1

            if global_step % eval_freq == 0:                                        #F
                train_loss, val_loss = evaluate_model(
                    model, train_loader, val_loader, device, eval_iter)
                train_losses.append(train_loss)
                val_losses.append(val_loss)
                track_tokens_seen.append(tokens_seen)
                print(f"Ep {epoch+1} (Step {global_step:06d}): "
                      f"Train loss {train_loss:.3f}, Val loss {val_loss:.3f}")

        generate_and_print_sample(                                                  #G
            model, tokenizer, device, start_context
        )
    return train_losses, val_losses, track_tokens_seen


#A 初始化用于记录损失和已处理 token 数量的列表
#B 开始主训练循环
#C 重置上一批次的损失梯度
#D 计算损失梯度
#E 使用损失梯度更新模型权重
#F 可选的评估步骤
#G 每个 epoch 结束后打印示例文本

附录

附录A. 联合概率分布、条件概率分布

llm 底层使用的是 联合概率分布、还是 条件概率分布？

这是一个很核心的问题。在 大语言模型（LLM） 的底层，本质上是基于 条件概率分布 的建模，而不是直接建联合概率。

A.1. 联合概率与条件概率的关系

\[P(x) = P(x_1, x_2, \dots, x_T)\] \[P(x) = \prod_{t=1}^T P(x_t \mid x_1, \dots, x_{t-1})\]

也就是说，模型不需要直接学整个联合分布，而是学每一步的条件概率。

A.2. LLM 的做法

大语言模型（GPT、LLaMA 等）实际上是：

训练时用 最大似然估计 (MLE)：

\[\max_\theta \sum_{t=1}^T \log P_\theta(x_t \mid x_1, \dots, x_{t-1})\]

这样，整个序列的联合概率就间接得到了（通过链式展开）。

A.3. 为什么不用直接建联合概率？

A.4. 总结：

附录B. LLM 本质是希望获取 联合概率分布

为什么希望用到联合概率分布呢？

这就涉及 “我们到底想从语言模型里得到什么”。

1. 联合概率分布的意义

如果我们真的有了完整的 联合概率分布 \(P(x_1, x_2, \dots, x_T)\)，那意味着：

2. 为什么现实里，不用直接建联合概率？

3. 条件概率的优势

通过 链式法则：

\[P(x_1, \dots, x_T) = \prod_{t=1}^T P(x_t \mid x_{<t})\]

我们只需学 条件概率分布：

4. 直观比喻

我们“希望”有联合概率分布，是因为它能完整刻画语言世界，任何 NLP 任务都能从它推导出来。

但现实做不到，所以 LLM 退而求其次，用 条件概率分解 来间接实现，对联合分布的建模。

5. 具体例子：联合概率 得到 条件概率

假设我们要把英文句子 \(E = (e_1, e_2, \dots, e_m)\) 翻译成中文句子 \(C = (c_1, c_2, \dots, c_n)\)。

如果我们掌握了联合概率分布：

\[P(E, C)\]

那翻译任务就可以直接写成一个 条件概率最大化问题：

\[C^* = \arg\max_{C} P(C \mid E) = \arg\max_{C} \frac{P(E, C)}{P(E)}\]

其中：

附录C. 梯度下降与反向传播

细节：AI 系列：反向传播 & 梯度下降

附录D. 最大似然估计（Maximum Likelihood Estimation, MLE）

其实是交叉熵损失背后的统计学含义。

下文拆开解释一下「最大似然估计（Maximum Likelihood Estimation, MLE）」在 LLM 训练中的意义：

1. 似然（Likelihood）的含义

在概率模型里，给定参数 (\(\theta\))，模型定义了一个概率分布 (\(P_\theta(x)\))。

当我们观察到训练数据 (\(x\)) 时，似然函数就是：

\[L(\theta; x) = P_\theta(x)\]

它表示 在参数 (\(\theta\)) 下，模型生成这批数据的概率有多大，即，x 表示输出结果。

2. 在 LLM 中的似然

对于一段文本序列：

\[x = (w_1, w_2, \dots, w_T)\]

语言模型假设序列的联合概率分布，是按条件概率分解的（复合函数的链式法则）：

\[P_\theta(x) = \prod_{t=1}^T P_\theta(w_t \mid w_{<t})\]

其中：

3. MLE 的训练目标

最大化似然，就是最大化所有训练样本的概率：

\[\theta^* = \arg\max_\theta \prod_{x \in D} P_\theta(x)\]

通常对数化（避免连乘数值下溢接近0）：

\[\theta^* = \arg\max_\theta \sum_{x \in D} \log P_\theta(x)\]

再代入链式展开：

\[\log P_\theta(x) = \sum_{t=1}^T \log P_\theta(w_t \mid w_{<t})\]

4. 与交叉熵的关系

你会发现：最大化对数似然 = 最小化交叉熵损失。

因为每个位置的损失是：

\[\text{Loss}*t = -\log P*\theta(w_t \mid w_{<t})\]

所以：

\[\text{Loss} = - \frac{1}{|D|} \sum_{x \in D} \sum_{t=1}^T \log P_\theta(w_t \mid w_{<t})\]

这就是「最小化交叉熵损失」的公式：所有训练集合 \(D\) 内序列 \(T\) 每次下一个 Token 预测损失函数之和。 （llm 下，单次token 预测中，损失函数：概率的负对数，有没求和。）

5. 直观理解

换句话说：LLM 训练目标是让模型成为“在训练语料中，最擅长预测下一个词的概率分布的参数集合”。

附录E. 框架下 CrossEntropyLoss 交叉熵计算细节

问题：DataLoader 参数中，常用的 Dataset 实现中，都是定义了一个滑动窗口，从中抽取出 input 和 label，并且 label 就是 input 平移一位之后的token序列，这是不是就说明：交叉熵损失，没有求和了？

回答：不对，也有求和；因为输入的是 token 序列，框架自动对序列求和了。

这个点你抓得很精准，分开来说清楚：

1. Dataset 层面

在 LLM 的自监督训练里，最常见的 Dataset 实现确实是：

这样，一个样本就是 一个完整的序列对 (input, label)。

2. Loss 计算层面

虽然 Dataset 提供的 label 是一个 token 序列，但在 forward + loss 的过程中，模型还是会对 序列中的每个位置计算交叉熵：

# 伪代码
logits = model(input_ids)  # shape: [batch, T, vocab_size]
loss = CrossEntropyLoss()(logits.view(-1, vocab_size), labels.view(-1))

这里的 CrossEntropyLoss 内部逻辑：

所以，序列内部的求和是仍然存在的，只是框架帮你完成了。

3. 为什么会感觉“没有求和”？

因为：

4. 类比一下

如果序列长 5，labels = [w2, w3, w4, w5, w6]，那 loss 实际上是：

\[\text{Loss} = \frac{1}{5}\Big( -\log P(w_2|w_1) -\log P(w_3|w_1,w_2) -\log P(w_4|w_1,w_2,w_3) -\log P(w_5|w_1,w_2,w_3,w_4) -\log P(w_6|w_1,w_2,w_3,w_4,w_5) \Big)\]

只是 PyTorch 自动聚合了。

5. 总结

6. 扩展

问题：能不能在 Dataset 里就把「labels = input.shift(-1)」这个逻辑做成默认行为，这样调用 Dataset 时只管传入 input 序列，不需要用户自己在业务代码里手动构造 label？

回答：完全可以，而且很多框架就是这么做的。

交叉熵损失只需要：

既然 labels 和 input 存在固定的变换关系，那 Dataset 层完全可以自动生成 labels，用户只传 input 就够了。很多 LLM 框架（比如 HuggingFace GPT2/LLama 的 model.forward）已经是这么干的了。

实际情况：

各种设计的差别：

原文地址：https://ningg.top/ai-series-build-llm-from-scratch/
微信公众号 ningg, 联系我

同类文章:

微信搜索: 公众号 ningg, 联系我, 交个朋友.

京ICP备19013747号-1
Top