AI 系列: 激活函数 & Softmax 函数
2025-04-12
激活函数(Activation Function)是神经网络中的核心组件,它的作用类似于神经元的“开关”或“过滤器”,负责决定神经元是否被激活(即输出信号)、以及激活的程度。以下是详细解释:
一、激活函数的含义与作用
- 核心功能:引入非线性
- 神经网络若只有线性运算(如矩阵乘法),无论叠加多少层,最终等效于一个
线性模型,无法学习复杂模式(如曲线、分类边界)。 - 激活函数对输入进行非线性变换,使神经网络具备
拟合任意函数的能力(万能逼近定理)。
示例: 输入 \(z = w_1x_1 + w_2x_2 + b\) → 输出 \(a = g(z)\)(\(( g )\) 为激活函数)。
- 神经网络若只有线性运算(如矩阵乘法),无论叠加多少层,最终等效于一个
- 生物启发:模拟神经元激活
- 名称“激活”源于生物神经元:当输入
信号超过阈值时,神经元“放电”(激活);否则静默。 - 激活函数类似:输入值 ( \(z\) ) 经过函数处理后,决定神经元输出强度(如 ReLU:( \(z>0\) ) 时输出 \(z\),否则输出 0)。
- 名称“激活”源于生物神经元:当输入
- 常见激活函数举例
在线绘图:https://www.geogebra.org/graphing?lang=zh_CN
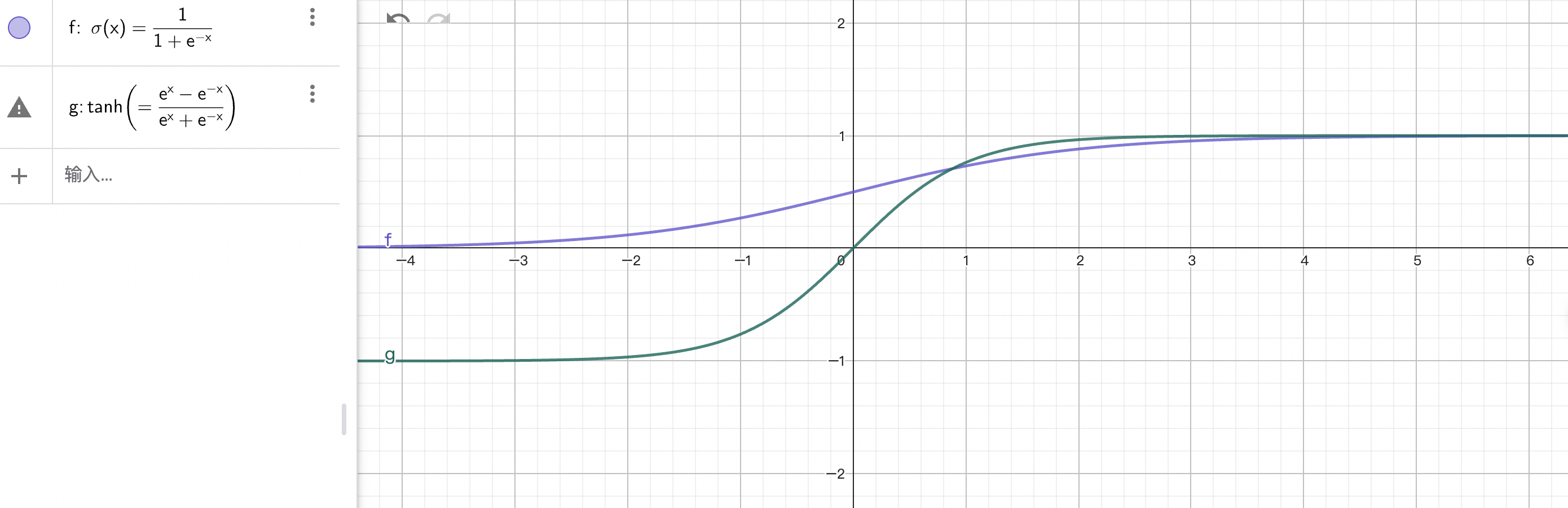
| 函数 | 公式 | 特点 |
|---|---|---|
| Sigmoid | \(\sigma(z) = \frac{1}{1+e^{-z}}\) | 输出 [0,1],适合二分类概率 |
| ReLU | \(\text{ReLU}(z) = \max(0, z)\) | 计算快,解决梯度消失(但可能有“死神经元”) |
| Tanh | \(\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\) | 输出 [-1,1],中心对称 |
ReLU的全称是Rectified Linear Unit(修正线性单元)。它的特点是:
- 当输入 \(x > 0\) 时,输出等于输入
- 当输入 \(x ≤ 0\) 时,输出为 0
ReLU 函数因其简单性和有效性而在深度学习中广泛使用,它解决了传统激活函数(如 sigmoid 和 tanh)的
梯度消失问题,并且计算效率很高。
二、Softmax 函数的本质与名称解析
1. 功能:多分类的概率归一化
- 场景:用于神经网络的最后一层,将原始输出分数(logits)转化为概率分布。
- 公式:
- 所有输出概率之和为 1 ( \(\sum \text{Softmax}(z_i) = 1\) )。
- 放大高分值的概率,抑制低分值(指数效应)。
2. 为什么叫 “Softmax”?
- “Max”:表示其倾向于选择最大值(概率最高的类别)。
- “Soft”:指它以概率形式输出最大值,而非直接硬性选择(如 “Hardmax”)。
对比示例:- 输入分数: \(z = [2.0, 1.0, 0.1]\)
- Hardmax(One-hot): \([1, 0, 0]\)
- Softmax: ≈ \([0.65, 0.24, 0.11]\)
→ Softmax 保留了概率信息(如第二类有 24% 可能性),而非武断判决。
3. 物理意义:置信度分布
在分类任务中,Softmax 输出的每个值表示模型对当前样本属于各类别的置信概率。
例如:图像分类输出 \([0.9, 0.08, 0.02]\) → 模型 90% 确信是“猫”。
三、激活函数的重要性总结
| 作用 | 说明 |
|---|---|
| 引入非线性 | 使神经网络能学习复杂模式(如曲线、决策边界)。 |
| 特征空间变换 | 将输入映射到更高维/可分空间(如 ReLU 的分段线性拟合)。 |
| 概率化输出 | 如 Softmax 将输出转为概率,支持分类决策。 |
| 梯度控制 | 合适的激活函数(如 ReLU)缓解梯度消失/爆炸问题,加速训练。 |
四、关键理解
- “激活”的本质:通过非线性函数决定神经元的输出强度(0 到 1、-1 到 1 或其他范围)。
- Softmax 的“Soft”:以概率形式实现“最大值选择”,保留不确定性信息,适用于多分类。
- 与 Hardmax 的区别:Hardmax(如
argmax)直接输出离散类别标签,Softmax 输出连续概率分布(更易优化)。
一句话总结:激活函数是神经网络的“非线性引擎”,赋予模型解决复杂问题的能力;Softmax 则是多分类任务的“概率转换器”,其“Soft”体现在以概率形式逼近最大值选择。
五、交叉熵对 logits 的导数
LLM 训练过程中,先计算交叉熵损失,再计算梯度:交叉熵对 logits 的导数,就是梯度。
把“公式推导”跟“业务直觉”联系起来。
1. 交叉熵损失 (Cross-Entropy Loss)
分类问题里最常见:
\[L = -\sum_{i=1}^C y_i \log p_i\]- \(C\):类别数
- \(y_i\):真实标签(
one-hot时只有一个 1,其余是 0) - \(p_i\):模型预测的概率(softmax 输出)
对 logits (\(z_i\))(softmax 前的分数)求导时:
\[\frac{\partial L}{\partial z_i} = p_i - y_i\]这就是交叉熵损失的梯度形式。
2.交叉熵损失的梯队推导
我们来完整推一遍 交叉熵对 logits 的导数,这样你就能直观理解为什么结果是 \(p_i - y_i\)。
1. 定义
Softmax 函数:
\[p_i = \frac{e^{z_i}}{\sum_{j=1}^C e^{z_j}}\]交叉熵损失(单分类 one-hot 标签):
\[L = -\sum_{i=1}^C y_i \log p_i\]其中:
- \(y_i\) 是 one-hot 向量(真实类别的那个位置 = 1,其余 = 0)。
- \(p_i\) 是预测概率(softmax 输出)。
2. 求导过程
我们想要求:
\[\frac{\partial L}{\partial z_i}\]第一步:对 \(p_i\) 的求导链式法则
第二步:先算 \((\frac{\partial L}{\partial p_k})\)
\[L = -\sum_{k=1}^C y_k \log p_k\]所以: \(\frac{\partial L}{\partial p_k} = -\frac{y_k}{p_k}\)
第三步:再算 \((\frac{\partial p_k}{\partial z_i})\)
softmax 的性质:
\[\frac{\partial p_k}{\partial z_i} = \begin{cases} p_i (1 - p_i), & k = i \\p_k p_i, & k \neq i \end{cases}\]这是因为 softmax 是向量函数,导数会出现这种 对角+非对角 形式。
第四步:合并
代入:
\[\frac{\partial L}{\partial z_i} = \sum_{k=1}^C \left(-\frac{y_k}{p_k}\right) \cdot \frac{\partial p_k}{\partial z_i}\]展开两部分:
-
当 (
k = i): \(-\frac{y_i}{p_i} \cdot p_i (1 - p_i) = -y_i (1 - p_i)\) -
当 (
k ≠ i): \(-\frac{y_k}{p_k} \cdot (-p_k p_i) = y_k p_i\)
合并:
\[\frac{\partial L}{\partial z_i} = -y_i (1 - p_i) + \sum_{k \neq i} y_k p_i\]因为 \(y\) 是 one-hot,(\(\sum_{k \neq i} y_k = 1 - y_i\))。 所以:
\[\frac{\partial L}{\partial z_i} = -y_i + y_i p_i + p_i (1 - y_i)\]化简:
\[\frac{\partial L}{\partial z_i} = p_i - y_i\]3. 直观解释
-
如果类别 i 是正确类别(\(y_i = 1\)): \((\frac{\partial L}{\partial z_i} = p_i - 1)\) → 预测越低,梯度越大(负数,推动往上调)。
-
如果类别 i 是错误类别(\(y_i = 0\)): \((\frac{\partial L}{\partial z_i} = p_i)\) → 预测越高,梯度越大(正数,推动往下调)。
所以它自动带有“推高正确类别,压低错误类别”的特性。
4. 总结
交叉熵 + softmax 的梯度: 天然简化成 (\(p_i - y_i\)),这就是为什么深度学习框架里常常直接写成一行代码 grad = p - y。
原文地址:https://ningg.top/ai-series-softmax-intro/